Угловые распределения продуктов тройного деления ядер в реакции  без учета кориолисова взаимодействия.

Рассмотрим реакцию  тройного деления ядра-мишени со спином , его проекцией  на ось  л.с.к. продольно-поляризованными холодными нейтронами с вылетом в качестве третьей частицы -частицы. Как было показано в работе , исследуемая реакция протекает преимущественно через формирование -нейтронных резонансов составного ядра в первой яме потенциала деформации, которые описываются волновыми функциями  со спином , его проекцией  на ось  л.с.к. и прочими квантовыми числами , включающими атомный вес  и заряд  составного ядра.

Для дальнейшего исследования воспользуемся результатами работ , в которых исследованы механизмы двойного и тройного деления ядер в рамках квантовомеханической теории деления ядер .

Рассмотрим эффективную волновую функцию составного ядра , которая определяется суперпозицией волновых функций нейтронных резонансов, возбуждаемых в исследуемой реакции , с нормировкой, учитывающей свойства входного нейтронного канала:

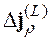                                                             (2.04)

где

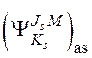                                                                       (2.05)

причем  – амплитуда нейтронной ширины распада -нейтронного резонанса,  – полная энергия делящейся системы в с.ц.м.,  и  – энергия и полная ширина распада -нейтронного резонанса. В формуле (2) учтена малость нейтронных потенциальных фаз рассеяния для холодных нейтронов. Многочастичная волновая функция нейтронного резонанса , соответствующая аксиально-симметричной форме составного ядра, из-за сильного влияния кориолисова взаимодействия представляет собой суперпозицию многоквазичастичных волновых функций составного ядра  с фиксированными значениями проекций  спина  на ось симметрии составного ядра, совпадающую с осью  внутренней системы координат (в.с.к.) этого ядра. Коэффициенты этой суперпозиции  имеют стохастический характер со средним значением модуля , равным , и случайным знаком. Для описания деления составного ядра из состояния с волновой функцией , в этой волновой функции можно выделить с амплитудой , имеющей стохастическую природу, коллективную колебательную компоненту, которая при эволюции делящегося ядра, связанной с изменением его параметров деформации при сохранении аксиальной симметрии, переходит с динамической амплитудой учитывающей структуру барьеров деления  в волновую функцию  определенной моды деления, которая описывает как предразрывную конфигурацию делящейся системы, так и ее характеристики в кластерной области, где уже сформированы первичные продукты деления. Этот процесс можно описать формулой вида:

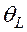,                                                 (2.06)

где амплитуда  определяется произведением введенных выше амплитуд:

                                            (2.07)

Оболочечная компонента волновой функции моды деления  может быть представлена в виде :

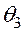(2.08)

где  – обобщенная сферическая функция, зависящая от углов Эйлера , характеризующих ориентацию внутренних осей делящегося ядра по отношению к осям л.с.к. Функция  совпадает с обращенной по времени внутренней волновой функцией , зависящей от набора внутренних координат ядра . Волновая функция моды деления  после разрыва делящегося ядра на первичные продукты тройного деления переходит в свою кластерную компоненту 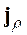, которая может быть представлена как :

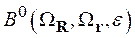,                                 (2.09)

где  – многочастичная функция Грина, зависящая от полных наборов координат  и  делящейся системы и описывающая эволюцию этой системы в кластерной области, которая при учете сильной связи каналов деления принимает вид :

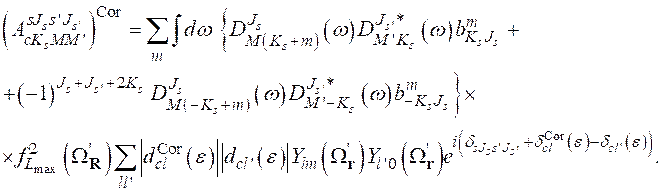                 (2.10)

где индекс   соответствует набору координат  или , включающему  большее (меньшее) из значений гипер-радиусов , , входящих в наборы координат , . Для нахождения явного выражения для функции Грина  (7) нормированные на -функцию по энергии регулярную и нерегулярную волновые функции  и , описывающие потенциальное рассеяние продуктов деления друг на друге, можно представить в виде разложения по каналовым функциям :

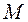                (2.11)

где  и  – регулярный и нерегулярный радиальные формфакторы, которые являются решениями системы связанных дифференциальных уравнений с граничными условиями, определенными в работе . Формфакторы  и  совпадают с обращенными по времени формфакторами , . Каналовая функция , входящая в формулу (2.11) имеет структуру:

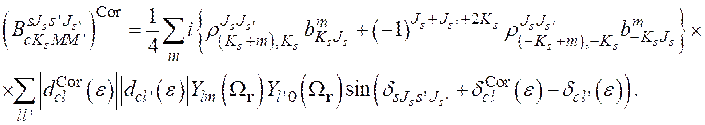                (2.12)

где радиусы-векторы  и  определяются как  и , причем , ,  – координаты центров тяжести фрагментов деления и -частицы, соответственно, , индекс , , , а телесные углы  и  определяют направления радиусов-векторов  и  в л.с.к. Координаты  и  связаны с гиперсферическими координатами  и  , при этом угол  () определяет асимптотическую энергию третьей частицы :

,                                           (2.13)

где , причем  – максимальная энергия третьей частицы: , а  – полная энергия относительного движения продуктов тройного деления в канале . Функции  выражаются через полиномы Якоби :

           (2.14)

где положительно определенная амплитуда парциальной делительной ширины  и потенциальная делительная фаза  определяются формулой:

                          (2.15)

В формуле (2.14) , , где  – эффективная масса продуктов тройного деления в канале .

Переводя функции  и  во в.с.к. делящегося ядра с помощью преобразования Вигнера при условии совпадения углов Эйлера  -го фрагмента деления с углами Эйлера  делящегося ядра, каналовую функцию (2.12) можно представить в форме :

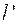      (2.16)

где в фигурной скобке оставлены только два из четырех членов, возникающих при умножении внутренних волновых функций фрагментов деления для , имеющих структуру вида (5). В формулах (9), (13) относительный орбитальный момент фрагментов деления  учитывает через закон сохранения полного спина делящейся системы влияние относительного орбитального момента  вылетающей -частицы. Поэтому естественно перейти в представление, в котором явно выделена часть  орбитального момента фрагментов деления , не зависящая от орбитального момента  -частицы. Для этого преобразуем сферическую функцию  в систему координат, связанную с радиусом-вектором :

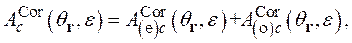                            (2.17)

где  – телесный угол, характеризующий направление радиуса-вектора  в указанной системе координат, и воспользуемся соотношением:

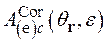                 (2.18)

Тогда при использовании формул (2.17), (2.18) и формулы:

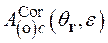                               (2.19)

каналовую функцию  (2.16) можно преобразовать к виду:

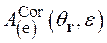(2.20)

Для построения амплитуды парциальной делительной ширины 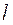 (2.15) при использовании для каналовой функции  и оболочечной компоненты 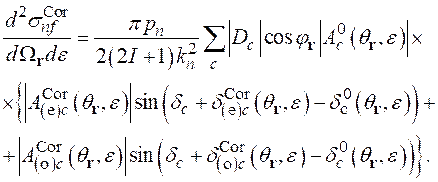 волновой функции моды деления формул (2.20) и (2.08) следует учесть тот факт, что из-за влияния сверхтекучих нуклон-нуклонных корреляций при формировании продуктов тройного деления и аксиально-симметричной структуры потенциалов взаимодействия -частицы с фрагментами тройного деления в сумме по  и  формулы (2.20) необходимо сохранить лишь члены с . 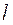Тогда величину  можно представить как :

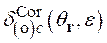      (2.21)

где из-за закона сохранения четности , где  и ,  – четности родительского ядра и фрагментов деления,  – действительные коэффициенты, определяющие нормированное на единицу угловое и энергетическое распределение -частиц, а  – функция Хевисайда, зависящая от максимального значения  относительного орбитального момента  фрагментов деления. Нормировочная константа в формуле (2.21) выбирается из условия, что квадрат положительно определенной величины  совпадает при определении асимптотического поведения волновой функции моды деления 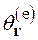 (2.14) с полной парциальной шириной  тройного деления в канал : .

Подставляя амплитуду (2.21) и каналовую функцию (2.20) в формулу (2.14), используя тот факт, что потенциальная делительная фаза  пренебрежимо слабо зависит от орбитальных моментов ,  и спинов , , ,   и поэтому ее можно представить как , учитывая что для достаточно больших значений , в полиноме  величину  можно заменить на некоторое усредненное значение , и проводя суммирование по , ,  с использованием соотношений:

,

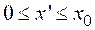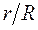
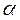, (2.22)

можно представить асимптотику волновой функции моды деления 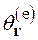 для канала деления с , , когда , как

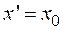      (2.23)

где фактор  имеет вид:

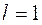                              (2.24)

причем

,                                (2.25)

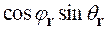,                      (2.26)

В формуле (2.23) фактор  определяет нормированное на единицу угловое и энергетическое распределение -частиц:

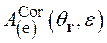                         (2.27)

причем

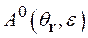,                          (2.28)

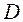                                       (2.29)

Формулу (2.23) можно преобразовать к форме, где разделены орбитальные движения фрагментов деления и -частицы. Для этого воспользуемся обратным по отношению к (2.17) преобразованием:

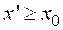.                                      (2.30)

Учитывая, что фактор  в зависимости от угла  имеет вид «размазанной» -функции, отличной от нуля в узкой окрестности угла , а величина , в формуле (2.30) можно положить угол  равным нулю, и воспользовавшись свойством обобщенной сферической функцией при =0 :

,                                                         (28)

получить для асимптотической волновой функции (2.30) при замене  на  новое выражение:

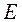      (2.32)

Подставляя волновую функцию (2.32) в формулу (2.04), вводя многомерный оператор плотности потока частиц  в направлении гипер-радиуса  и проводя интегрирование по внутренним координатам , ,  продуктов деления и углам Эйлера , можно получить формулу для тройного дифференциального сечения реакции :

,                                  (2.33)

где  – волновой вектор налетающего нейтрона, а величина  имеет вид:

   (2.34)

В формуле (2.33) величины  и   определяются как:

,                                       (2.35)

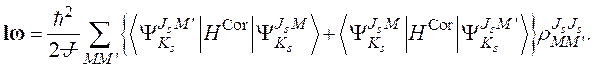.            (2.36)

Величина , входящая в формулу (2.36), имеет структуру:

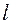                                                             (2.37)

причем фаза  имеет вид:

                                        (2.38)

а фаза , связанная с нейтронным резонансом , определяется как

                                                                                                                                                         (2.39)

В формулу (2.36) входит спиновая матрица плотности , учитывающая интерференцию делительных амплитуд различных -нейтронных резонансов  и  и построенная в работе для случая направления вектора поляризации нейтрона  по оси  л.с.к. :

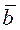                                                                             (2.40)

где фактор  имеет структуру:

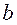               (2.41)

причем , .

Проведем в формуле (2.37) преобразование шаровой функции  в л.с.к., используя преобразование Вигнера:

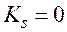.                         (2.42)

Выберем ось  л.с.к. по направлению вылета легкого фрагмента тройного деления. Используя результаты работы , можно показать, что для тройного деления угол  между указанным направлением и направлением радиуса-вектора  в асимптотической области из-за малостей массы -частицы по сравнению с массами фрагментов деления и кинетической энергии -частицы по сравнению с кинетическими энергиями фрагментов имеет малое значение и не превосходит величины , соответствующей максимальной энергии -частицы  МэВ. Тогда с точностью до малых поправок, связанных с эффектом отдачи центра тяжести фрагментов деления из-за вылета -частицы, вектор  будет также совпадать с осью . В этом случае функцию , близкую к боровскому пределу из-за большого значения , можно с высокой точностью представить через сумму -функций вида :

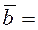,                                  (2.43)

где  – второй угол Эйлера из набора углов . При подстановке формулы (2.42) в формулу (2.37) и проведении интегрирования по  с учетом свойств функций Вигнера:

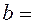,                         (2.44)

можно убедиться, что полученное выражение для фактора  будет диагонально по индексам , . Но тогда зависящая от поляризации нейтрона часть 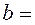 матрицы плотности ядра , которая определяется вторым членом формулы (2.40) и имеет только недиагональные по индексам ,  компоненты, не даст вклада в величину (2.36) и, следовательно, в дифференциальное сечение реакции  (2.33). Проводя интегрирование по  в формуле (2.37) при использовании формул (2.43), (2.44) величину  (2.36) при учете формулы (2.40) можно представить как:

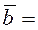(2.45)

В этом случае трижды дифференциальное сечение реакции  (2.33) приводится к дважды дифференциальному сечению 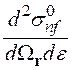, которое определяется как

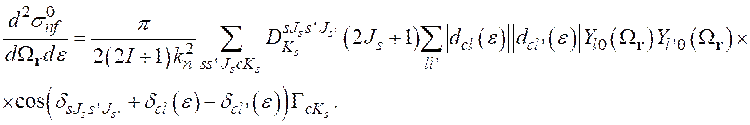 (2.46)

Если ввести определение амплитуды  углового и энергетического распределения - частиц как

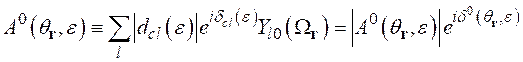,                (2.47)

то формулу (2.46) можно преобразовать к виду:

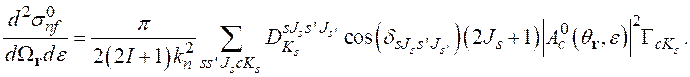                (2.48)

Для наиболее вероятных фрагментов тройного деления, обладающих близкими зарядовыми и массовыми асимметриями, амплитуда  слабо зависит от индекса , и поэтому сечение (2.48) можно представить в факторизованной форме, пропорциональной 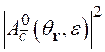, где  – некое усредненное значение каналового индекса. Как следует из эксперимента по тройному делению ядер неполяризованными холодными нейтронами, амплитуда  имеет гауссовскую форму с максимумом, сдвинутым относительно угла  на сравнительно малый угол, обусловленный влиянием зарядовой и массовой асимметрии для наиболее вероятных фрагментов тройного деления.