Волновые функции делящейся системы с учетом Кориолисова  взаимодействия

В работе на основе анализа механизмов тройного деления ядер и структуры потенциалов взаимодействия продуктов тройного деления было показано, что движение - частицы в делящейся системе может рассматриваться как ее движение в поле растягивающейся аксиально-симметричной «гантели», образуемой соосными фрагментами деления. При этом вся делящаяся система вращается как единое целое. Поэтому для описания углового и энергетического распределения продуктов тройного деления можно использовать обобщенную модель ядра и дополнить гамильтониан делящегося ядра  гамильтонианом , связанным с кориолисовым взаимодействием продуктов деления со спином  делящейся системы :

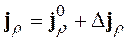                                   (2.49)

где  – оператор полного спина продуктов тройного деления, действующий во в.с.к. делящегося ядра, а операторы ,  определяются как

, ,                                  

где ,  и ,  индексы осей лабораторной и внутренней систем соответственно. Гамильтониан  (2.49) в энергетической шкале значительно меньше входящих в гамильтониан  операторов относительных кинетических энергий и потенциалов взаимодействия продуктов тройного деления. Поэтому учет влияния кориолисова взаимодействия можно провести в первом порядке теории возмущений. При использовании представлений работы можно показать, что действие оператора  на внутренние волновые функции продуктов тройного деления, обладающих спинами , ,  соответственно, приводит к появлению состояний, внутренние волновые функции которых ортогональны соответствующим волновым функциям невозмущенных кориолисовым взаимодействием состояний делящейся системы. Поэтому интерференция делительных амплитуд невозмущенных и возмущенных подобным образом при учете кориолисова взаимодействия состояний делящейся системы отсутствует, так что влиянием  на внутренние волновые функции продуктов деления можно пренебречь. В этом случае в формуле (2.49) следует сохранить только члены, связанные с операторами относительных орбитальных моментов фрагментов деления  и третьей частицы . Действие операторов  на обобщенные сферические функции  и операторов  и  на сферические функции  и  определяется формулами :

                    ,           (2.50)

,.

Значение момента инерции  делящейся системы, фигурирующего в формуле (2.49), меняется при разлете продуктов деления от значения момента инерции делящегося ядра в предразрывной конфигурации до значения  при , где  – приведенная масса фрагментов деления в анализируемом канале деления .

Для учета влияния кориолисова взаимодействия на волновую функцию делящейся системы в кластерной области 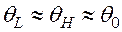 все члены формулы (2.09), не возмущенные кориолисовым взаимодействием, а именно – функцию Грина , гамильтониан делящейся системы  и оболочечную компоненту волновой функции моды деления 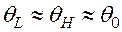, следует заменить на искаженные кориолисовым взаимодействием в первом порядке теории возмущений соответствующие члены: ; ; 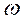. Тогда невозмущенная кластерная компонента волновой функции моды деления  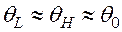(2.09) заменяется на возмущенную кориолисовым взаимодействием кластерную компоненту 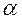, имеющую структуру 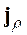, причем величина  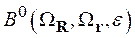определяется как

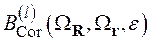. (2.51)

Поскольку функци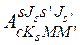и  и 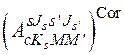 при учете влияния кориолисова взаимодействия (2.45) характеризуются проекциями  спина делящейся системы , равными , а невозмущенная функция Грина  определяется аналогичными проекциями, равными , то второй и третий члены в формуле (2.47) равны нулю, и эта формула преобразуется к виду:

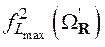.                               (2.52)

Учитывая, что поправка к функции Грина , связанная с влиянием кориолисова имеет вид:

,                                  (2.53)

где функция Грина  учитывает перестройку структуры входящих в нее каналовых функций  по сравнению со структурой каналовых функций , входящих в определение невозмущенной кориолисовым взаимодействием функции Грина , изменение кластерной волновой функции делящейся системы (48) в асимптотической области при , обусловленное влиянием кориолисова взаимодействия, можно представить как

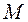. (2.54)

Тогда, учитывая, что полная асимптотическая функция 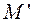 делящейся системы имеет структуру: 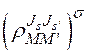, величину плотности потока  продуктов деления в направлении гипер-радиуса  в первом порядке по кориолисову взаимодействию можно представить в виде: , где величина  определяется невозмущенной функцией 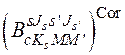, а величина , характеризующая влияние кориолисова взаимодействия на угловые и энергетические распределения продуктов деления, связана с интерференцией функций  и .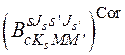

Для построения функции 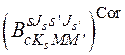 (2.53) исследуем структуру кластерной компоненты невозмущенной волновой функции делящегося ядра  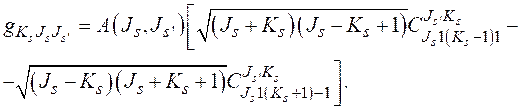в точке  с конечным значением гипер-радиуса  на основе преобразований, использованных выше для получения асимптотической функции  (2.23). В этом случае функция 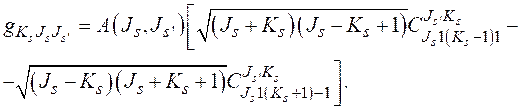 может быть представлена формулой (2.29) при замене функции  на функцию  и амплитуды  на амплитуду , отличающуюся от  введением в функцию Хевисайда вместо  величины . При этом в асимптотической области  () функция  и величина  переходят в предельные значения , .

Исследуем теперь действие на определенную таким образом волновую функцию 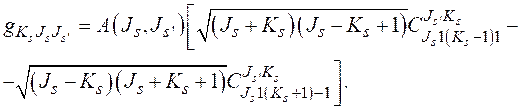  кориолисова гамильтониана  (2.49), который представим в виде , где операторы  и  определяются членами формулы (2.48), связанными с операторами  и  соответственно. Тогда для функции 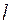 возникает формула

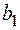                        (2.55)

где , а величины  и  имеют вид:

;  ,   (2.56)

Аналогично для функции 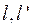 можно получить формулу:

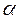               (2.57)

Теперь можно рассчитать поведение функции 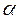 (2.54), которое определяется эволюцией перестроенных под действием кориолисова взаимодействия функций  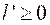(2.55) и  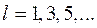(2.56) в области , определяемой интегралом перекрытия этих функций с функцией Грина , учитывающей только потенциалы взаимодействия продуктов деления между собой. Из-за аксиальной симметрии указанных потенциалов проекции  орбитальных моментов фрагментов деления и -частицы на ось симметрии делящегося ядра будут сохраняться и в функции Грина  как интегралы движения во всей области . При использовании методов, развитых выше при построении невозмущенной кориолисовым взаимодействием функции 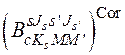 (2.32), функцию 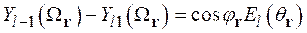, связанную формулой (2.54) с функцией  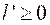(2.55), после интегрирования по  можно представить в виде:

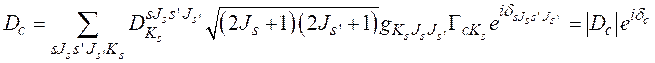              (2.58)

где комплексная амплитуда  эффективно учитывает влияние факторов 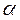 и , входящих в формулу (2.55), и характер движения -частицы при выключении кориолисова взаимодействия в области  с фиксированной проекцией  ее орбитального момента , меняющегося из-за взаимодействии этой частицы с фрагментами деления.

Аналогично, асимптотическую функцию 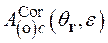, связанную формулой (2.54) с функцией  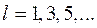(2.57), можно представить формулой вида

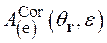           (2.59)

где  и  – амплитуды, описывающие асимптотическое распределение относительных орбитальных моментов фрагментов деления и -частицы, при учете действия компоненты кориолисова гамильтониана  на орбитальное движение фрагментов деления.