Вывод уравнения Ван-дер-Ваальса.

Как уже указывалось, для реальных газов необходимо учитывать размеры молекул и их взаимодействие друг с другом, поэтому модель идеального газа и уравнение состояния Клапейрона—Менделеева   (для моля газа) для реальных газов непригодны.

Учитывая собственный объем молекул и сил межмолекулярного взаимодействия, голландский физик И. Ван-дер-Ваальса (1837—1923) вывел уравнения состояния реального газа. Ван-дер-Ваальс для вывода использовал уравнение Клапейрона—Менделеева в которое ввел две поправки, учитывающие объем молекул и силы из взаимодействия.

1. Учет собственного объема молекул. Наличие сил отталкивания, которые противодействуют проникновению в занятый молекулой объем других молекул, сводится к тому, что фактический свободный объем, в котором могут двигаться молекулы реального газа, будет не , a , где  — объем, занимаемый самими молекулами. Объем  равен учетверенному собственному объему молекул. Если, например, в сосуде находятся две молекулы, то центр любой из них не может приблизиться к центру другой молекулы на расстояние, меньшее диаметра  молекулы. Это означает, что для центров обеих молекул оказывается недоступным сферический объем радиуса , т. е. объем, равный восьми объемам молекулы, а в расчете на одну молекулу — учетверенный объем молекулы.

2. Учет притяжения молекул. Действие сил притяжения газа приводит к появлению дополнительного давления на газ, называемого внутренним давлением. По вычислениям Ван-дер-Ваальса, внутреннее давление обратно пропорционально квадрату молярного объема, т. е.

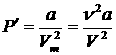,                                                                            (2.1)

где  — постоянная Ван-дер-Ваальса, характеризующая силы межмолекулярного притяжения,  — молярный объем.

Вводя эти поправки, получим уравнение Ван-дер-Ваальса для моля газа (уравнение состояния реальных газов):

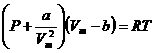.                                                      (2.2)

Для произвольного количества вещества  газа  с учетом того, что ,  уравнение Ван-дер-Ваальса примет вид

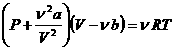                                                  (2.3)

где поправки  и  — постоянные для каждого газа величины, определяемые опытным путем (записываются уравнения Ван-дер-Ваальса для двух известных из опыта состояний газа и решаются относительно а и b).

При выводе уравнения Ван-дер-Ваальса сделан целый ряд упрощений, поэтому оно также весьма приближенное, хотя и лучше (особенно для несильно сжатых газов) согласуется с опытом, чем уравнение состояния идеального газа.

Ван-дер-Ваальса не единственное уравнение, описывающее реальные газы. Существуют и другие уравнения, некоторые из них даже точнее описывают реальные газы, но не рассматриваются из-за их сложности.