Применим полученные выше результаты для энергии электромагнитного поля к процессам передачи энергии.
Основной вывод, который можно сделать из (7.20), это то, что энергией обладают не заряды на проводниках, а электрическое и магнитное поле, распределенное в пространстве. Мощность передаваемой энергии определяется не непосредственно током или напряжением, а потоком вектора 
.
Рассмотрим это вначале на примере стационарных полей.
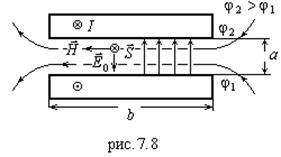Пусть два провода проходят в направлении, перпендикулярном плоскости рис.7.8. В одном проводе ток идет к потребителю, а в другом – обратно к источнику. Напряженность электрического поля между проводами:
,
где 
- разность потенциалов. Напряженность магнитного поля найдем по теореме о циркуляции:
; 
,
где 
и 
- размеры, показанные на рис.7.8. Вектор 
параллелен оси поводов и направлен к потребителю. Поток по всему сечению 
равен:
,
т.е. совпадает с передаваемой мощностью.
Одинаковый результат достигнут при различных физических картинах. В случае 
передача энергии идет по проводам. В случае 
энергия идет вне провода, причем плотность потока энергии в любой точке пространства определяется вектором .
В предыдущем рассмотрении мы считали проводники идеальными, поэтому электрическое поле внутри проводника отсутствует: 
. Если учесть проводимость проводника, то:
.
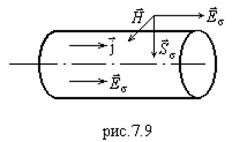Видно, что появилась составляющая 
, направленная так же, как ток 
. В силу теоремы о циркуляции:
Þ
,
т.е. точно такое же поле существует вне проводника. Тогда появляется вектор 
, направленный по радиусу к оси проводника (рис.7.9).
Найдем 
по теореме о циркуляции для проводника круглого сечения:
; 
.
Тогда:
.
Через боковую поверхность на длине 
втекает мощность:
,
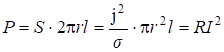где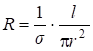 
- сопротивление проводника.
Джоулево тепло (5.10), выделяемое на длине проводника в 1 секунду:
.
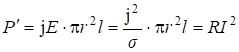Таким образом, 
, т.е. при прохождении постоянного электрического тока через проводник с удельным сопротивлением 
выделяемая в виде теплоты энергия поступает через боковую поверхность из окружающего пространства, где движется энергия электрического и магнитного полей.
Введем следующие обозначения:
- это поток энергии, передаваемой потребителю; 
- потери на джоулево тепло в подводящих проводах. Суммарный вектор (рис.7.10,а):
 |
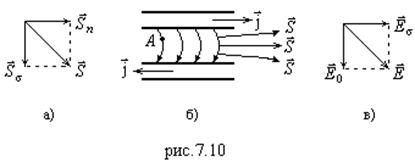должен быть перпендикулярен силовым линиям электрического поля. Ясно, что реальная картина силовых линий отлична от приведенной ранее на рис.7.8 и выглядит, как на рис.7.10, б. В точке А векторы напряженности электрического поля направлены так, как на рис.7.10, в, где вектор
характеризует поле в отсутствие потерь на сопротивление проводов. Из рис.7.10, б видно, что потери приводят к отклонению от направления вдоль длины провода. Понятно, что в случае переменного тока малой (промышленной) частоты картина качественно не изменится. Мощность передаваемой энергии определяется потоком 
и распространяется вне провода вдоль него. В случае двухпроводной линии используемая потребителем (полезная) мощность движется параллельно проводам в пространстве между ними. Потери на джоулево тепло в проводах определяются поступающей через боковую поверхность провода энергией.
Отличие от постоянного тока в том, что при определении нужно учесть разность фаз 
между током и напряжением. При
.
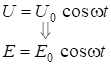
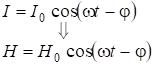Тогда: 
. Среднее по времени: 
. Подставляя вместо 
их значения 
, получим поток через сечение 
, т.е.:
, (7.23)
что совпадает с формулой для мощности переменного тока.
Поможем написать любую работу на аналогичную тему