Факторные планы

Факторные эксперименты применяются тогда, когда необходимо проверить сложные гипотезы о взаимосвязях между переменными. Общий вид подобной гипотезы; «Если A1 ..А2…. Ап, то В». Такие гипотезы называются комплексными, комбинированными и др. При этом между независимыми переменными могут быть различные отношения; конъюнкции, дизъюнкции, линейной независимости, аддитивные или мультипликативные и др. Факторные эксперименты являются частным случаем многомерного исследования, входе проведения которого пытаются установить отношения между несколькими независимыми и несколькими зависимыми переменными. В факторном эксперименте проверяются одновременно, как правило, два типа гипотез:

1)    гипотезы о раздельном влиянии каждой из независимых переменных;

2)    гипотезы о взаимодействии переменных, а именно — как присутствие одной из независимых переменных влияет на эффект воздействия на другой. Факторный эксперимент строится по факторному плану. Факторное планирование эксперимента заключается в том, чтобы все уровни независимых переменных сочетались друг с другом. Число экспериментальных групп равно числу сочетаний уровней всех независимых переменных.

Сегодня факторные планы наиболее распространены в психологии, поскольку простые зависимости между двумя переменными в ней практически не встречаются.

Существует множество вариантов факторных планов, но на практике применяются далеко не все. Чаще всего используются факторные планы для двух независимых переменных и двух уровней типа 2 х 2. Для составления плана применяется принцип балансировки. План 2x2 используется для выявления эффекта воздействия двух независимых переменных на одну зависимую. Экспериментатор манипулирует возможными сочетаниями переменных и уровней. Данные приведены в простейшей таблице (табл. 5.6).

Реже используются четыре независимые рандомизированные группы. Для обработки результатов применяется дисперсионный анализ по Фишеру.

Так же редко используются другие версии факторного плана, а именно: 3x2 или 3x3. План 3x2 применяется в тех случаях, когда нужно установить вид зависимости одной зависимой переменной от одной независимой, а одна из независимых переменных представлена дихотомическим параметром. Пример такого плана — эксперимент по выявлению воздействия внешнего наблюдения на успех решения интеллектуальных задач. Первая независимая переменная варьируется просто: есть наблюдатель, нет наблюдателя. Вторая независимая переменная — уровни трудности задачи. В этом случае мы получаем план 3x2 (табл, 5.7).

Вариант плана 3x3 применяется в том случае, если обе независимые переменные имеют несколько уровней и есть возможность выявить виды связи зависимой

Таблица 5.6

Таблица 5.7

Таблица 5.8

переменной от независимых. Этот план позволяет выявлять влияние подкрепления на успешность выполнения заданий разной трудности (табл. 5.8).

В общем случае план для двух независимых переменных выглядит как N x M. Применимость таких планов ограничивается только необходимостью набора большого числа рандомизированных групп. Объем экспериментальной работы чрезмерно возрастает с добавлением каждого уровня любой независимой переменной.

Планы, используемые для исследования влияния более двух независимых переменных, применяются редко. Для трех переменных они имеют общий вид L x M x N.

Чаще всего применяются планы 2x2x2: «три независимые переменные — два уровня». Очевидно, добавление каждой новой переменной увеличивает число групп. Общее их число 2, где п — число переменных в случае двух уровней интенсивности и К — в случае К-уровневой интенсивности (считаем, что число уровней одинаково для всех независимых переменных). Примером этого плана может быть развитие предыдущего. В случае, когда нас интересует успешность выполнения экспериментальной серии заданий, зависящая не только от общей стимуляции, которая производится в форме наказания — удара током, но и от соотношения поощрения и наказания, мы применяем план 3x3x3.

Таблица 5.9

Упрощением полного плана с тремя независимыми переменными вида L x M x N является планирование по методу «латинского квадрата». «Латинский квадрат» применяют тогда, когда нужно исследовать одновременное влияние трех переменных, имеющих два уровня или более. Принцип «латинского квадрата» состоит в том, что два уровня разных переменных встречаются в экспериментальном плане только один раз. Тем самым процедура значительно упрощается, не говоря о том, что экспериментатор избавляется от необходимости работать с огромными выборками.

Предположим, что у нас есть три независимые переменные, с тремя уровнями каждая:

1.  L1 L2 L3

2.   M 1 M2, M3

3.   А, В, С

План по методу «латинского квадрата» представлен в табл. 5.9.

Такой же прием используется для контроля внешних переменных (контрбалансировка). Нетрудно заметить, что уровни третьей переменной N (А, В, С,) встречаются в каждой строке и в каждой колонке по одному разу. Комбинируя результаты по строкам, столбцам и уровням, можно выявить влияние каждой из независимых переменных на зависимую, а также степень попарного взаимодействия переменных.

«Латинский квадрат» позволяет значительно сократить число групп. В частности, план 2x2x2 превращается в простую таблицу (табл. 5.10).

Применение латинских букв в клеточках для обозначения уровней 3-й переменной (А — есть, В — нет) традиционно, поэтому метод назван «латинский квадрате.

Более сложный план по методу «греко-латинского квадрата» применяется очень редко. С его помощью можно исследовать влияние на зависимую переменную четырех независимых. Суть его в следующем: к каждой латинской группе плана с тремя переменными присоединяется греческая буква, обозначающая уровни четвертой переменной.

Рассмотрим пример. У нас четыре переменные, каждая из которых имеет три уровня интенсивности. План по методу «греко-латинского квадрата» примет такой вид (табл. 5.11).

Для обработки данных применяется метод дисперсионного анализа по Фишеру. Методы «латинского» и «греко-латинского» квадрата пришли в психологию из агробиологии, но большого распространения не получили. Исключением являются некоторые эксперименты в психофизике и психологии восприятия.

Главная проблема, которую удается решить в факторном эксперименте и невозможно решить, применяя несколько обычных экспериментов с одной независимой переменной, — определение взаимодействия двух переменных.

Таблица 5.10

Таблица 5.11

Рассмотрим возможные результаты простейшего факторного эксперимента 2x2 с позиций взаимодействий переменных. Для этого нам надо представить результаты опытов на графике, где по оси абсцисс отложены значения первой независимой переменной, а по оси ординат — значения зависимой переменной. Каждая из двух прямых, соединяющих значения зависимой переменной при разных значениях первой независимой переменной (А), характеризует один из уровней второй независимой переменной (В). Применим для простоты результаты не экспериментального, а корреляционного исследования. Условимся, что мы исследовали зависимость статуса ребенка в группе от состояния его здоровья и уровня интеллекта. Рассмотрим варианты возможных отношений между переменными.

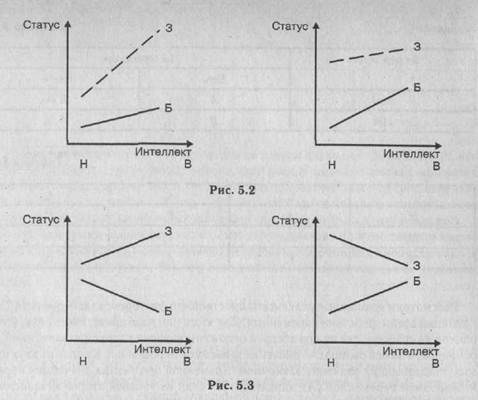
Первый вариант: прямые параллельны — взаимодействия переменных нет.

Больные дети имеют более низкий статус, чем здоровые, независимо от уровня интеллекта. Интеллектуалы имеют всегда более высокий статус (независимо от здоровья).

Второй вариант: физическое здоровье при наличии высокого уровня интеллекта увеличивает шанс получить более высокий статус в группе.

В этом случае получен эффект расходящегося взаимодействия двух независимых переменных. Вторая переменная усиливает влияние первой на зависимую переменную.

Третий вариант: сходящееся взаимодействие — физическое здоровье уменьшает шанс интеллектуала приобрести более высокий статус в группе. Переменная «здоровье» уменьшает влияние переменной «интеллект» на зависимую переменную. Есть и другие случаи этого варианта взаимодействия: переменные взаимодействуют так, что увеличение значения первой приводит к уменьшению влияния второй с изменением знака зависимости (рис. 5.3).

У больных детей, обладающих высоким уровнем интеллекта, меньше шанс получить высокий статус, чем у больных детей с низким интеллектом, а у здоровых — связь интеллекта и статуса позитивная.

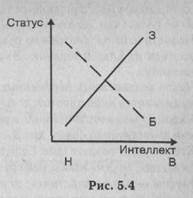
Теоретически возможно представить, что больные дети будут иметь больший шанс получить высокий статус при высоком уровне интеллекта, чем их здоровые низкоинтеллектуальные сверстники.

Последний, четвертый, возможный вариант наблюдаемых в исследованиях отношений между независимыми переменными: случай, когда между ними существует пересекающееся взаимодействие (Рис. 5.4).

Итак, возможны следующие взаимодействия переменных: нулевое; расходящееся (с различными знаками зависимости); пересекающееся.

Оценка величины взаимодействия проводится с помощью дисперсионного анализа, а t-критерий Стьюдента используется для оценки значимости различий групповых Хср.

Во всех рассмотренных вариантах планирования эксперимента применяется способ балансировки: различные группы испытуемых ставятся в разные экспериментальные условия. Процедура уравнивания состава групп позволяет производить сравнение результатов.

Однако во многих случаях требуется планировать эксперимент так, чтобы все его   Статус участники получили все варианты воздействия независимых переменных. Тогда на помощь приходит техника контрбалансировки.

Планы, в которых воплощается стратегия «все испытуемые — все воздействия», Мак-Колл называет ротационными экспериментами, а Кэмпбелл— «сбалансированными планами». Чтобы не было путаницы между понятиями «балансировка» и «контрбалансировка», будем использовать термин «ротационный план».

Ротационные планы строятся по методу «латинского квадрата», но, в отличие от рассмотренного выше примера, по строкам обозначены группы испытуемых, а не уровни переменной, по столбцам — уровни воздействия первой независимой переменной (или переменных), в клеточках таблицы — уровни воздействия второй независимой переменной.

Пример экспериментального плана для 3 групп (Л, В, С) и 2 независимых переменных (X, У) с 3 уровнями интенсивности (1-й, 2-й, 3-й) приводим ниже. Нетрудно заметить, что этот план можно переписать и так, чтобы в клеточках стояли уровни переменной Y (табл. 5.12).

Таблица 5.12

Кэмпбелл включает этот план в число квазиэкспериментальных на основании того, что неизвестно, контролируется ли с его помощью внешняя валидность. Действительно, вряд ли в реальной жизни испытуемый может получить серию таких воздействий, как в эксперименте.

Что касается взаимодействия состава групп с другими внешними переменными, источниками артефактов, то рандомизация групп, согласно утверждению Кэмпбелла, должна минимизировать влияние этого фактора.

Суммы по столбцам в ротационном плане свидетельствуют о различиях в уровне эффекта при разных значениях одной независимой переменной (X или Y), а суммы по строкам должны характеризовать различия между группами. Если группы рандомизированы удачно, то межгрупповых различий быть не должно. Если же состав группы является дополнительной переменной, возникает возможность ее проконтролировать. Схема контрбалансировки не позволяет избежать эффекта тренировки, хотя данные многочисленных экспериментов с применением «латинского квадрата» не позволяют делать такой вывод.

Подводя итог рассмотрению различных вариантов экспериментальных планов, предлагаем их классификацию. Экспериментальные планы различаются по таким основаниям:

1.    Число независимых переменных: одна или больше. В зависимости от их числа применяется либо простой, либо факторный план.

2.    Число уровней независимых переменных: при 2 уровнях речь идет об установлении качественной связи, при 3 и более — количественной связи.

3.    Кто получает воздействие. Если применяется схема «каждой группе — своя комбинация», то речь идет о межгрупповом плане. Если же применяется схема «все
группы — все воздействия», то речь идет о ротационном плане. Готтсданкер называет его кросс-индивидуальным сравнением.

Схема планирования эксперимента может быть гомогенной или гетерогенной {в зависимости от того, равно или не равно число независимых переменных числу уровней их изменения).