Для оценки динамики численности населения используют абсолютные показатели (абсолютный прирост или сокращение) и относительные показатели динамики (темпы роста или снижения и темпы прироста или сокращения).
Рассчитываются показатели динамики следующим образом.
Абсолютный прирост (сокращение) численности населения – разность между данными о численности населения на конец и начало исследуемого периода (например, года).
Темп роста (снижения) численности населения – отношение данных о численности населения на конец исследуемого периода (например, года) к данным о численности населения на начало исследуемого периода, выраженное в %.
Темп прироста (сокращения) – темп роста (снижения) минус 100%.
При расчёте темпов роста (прироста) предварительно рассчитывают коэффициенты роста (прироста), которые в анализе динамики численности населения могут иметь самостоятельное значение.
Приведём некоторые данные из истории роста численности населения Земли. В 1000г. во всём Мире насчитывалось 250 – 300 млн. человек, а
первый млрд. человек был зафиксирован в 1820г.;
второй – в 1927г. (через 107 лет);
третий – в 1960г. (через 33года);
четвёртый – в 1974г. (через 14 лет);
пятый – в 1987г. (через 13 лет);
шестой – в 1999г. (через 12лет).
Эти данные свидетельствуют о том, что численность населения Мира росла ускоренными темпами. Особенно её бурный рост пришёлся на 20 век.
Однако при более подробном изучении динамики численности населения Мира второй половины 20 века (см. таблицу 3.1) видим, что после 1970 г. численность населения Мира продолжала расти, но уже замедленными темпами.
Таблица 3.1
Динамика численности населения Мира второй половины 20 века
|
Годы |
Численность населения, млн. чел. |
Темп роста (цепной) |
Темп прироста (цепной) |
|
1950 |
2520 |
- |
- |
|
1960 |
3020 |
119,84 |
19,84 |
|
1970 |
3700 |
122,52 |
22,52 |
|
1980 |
4450 |
120,27 |
20,27 |
|
1990 |
5290 |
118,88 |
18,88 |
|
2000 |
6060 |
114,56 |
14,56 |
Задание 3.3. По данным таблицы 3.2, характеризующей изменение численности постоянного населения по годам в области, требуется определить:
1. Базисные темпы роста и прироста.
2. Среднегодовые цепные темпы роста и прироста.
Таблица 3.2
Изменение численности постоянного населения в области*
|
Показатели |
Годы |
|||
|
2005 |
2006 |
2007 |
2008 |
|
|
Сокращение численности населения в % к предыдущему году |
-1,0 |
-1,3 |
-1,8 |
-1,6 |
*Исходные данные условные.
Решение:
1. Базисные коэффициенты роста для i-го уровня:
, (3.1)
где 
- первый уровень ряда динамики;
- цепной коэффициент роста для i-го уровня;
- базисный коэффициент роста для (i – 1)-го уровня.
По условию задания нам даны цепные темпы сокращения. Чтобы от них перейти к цепным темпам снижения, надо использовать известные формулы:
, отсюда (3.2)
(3.3)
При этом помним, что если требуется перейти к коэффициентам, то темпы роста (снижения), как и темпы прироста (сокращения), надо разделить на 100 (и наоборот).
Тогда базисные коэффициенты роста (
):
-для 2006 г.: 
;
-для 2007 г.: 
;
-для 2008 г.: 
.
Результаты расчётов представлены в таблице 3.3.
Таблица 3.3
Показатели динамики численности населения
|
Показатели |
Годы |
|||
|
2005 |
2006 |
2007 |
2008 |
|
|
1. Темп сокращения цепной, % |
-1,0 |
-1,3 |
-1,8 |
-1,6 |
|
2. Темп снижения цепной, % |
99,0 |
98,7 |
98,2 |
98,4 |
|
3. Темп снижения базисный, % |
99,0 |
97,7 |
95,9 |
94,4 |
|
4. Темп сокращения базисный, % |
-1,0 |
-2,3 |
-4,1 |
-5,6 |
2. Среднегодовые коэффициенты роста в цепном варианте рассчитываются по следующей формуле:
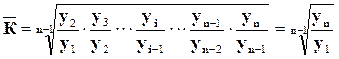, (3.4)
где n – число уровней ряда динамики (в нашей задаче их 5);
– базисный коэффициент роста, рассчитанный для последнего уровня ряда динамики (в нашей задаче он равен 0,944).
, отсюда
,
т.е. численность населения области с 2005 г. по 2008 г. сокращалось в среднем за год на 1,43%.
Поможем написать любую работу на аналогичную тему