Понятие коэффициента корреляции. Виды коэффициентов корреляции и специфика их применения в социологическом исследовании.

Коэффициенты корреляции используются для оценки силы связи между двумя признаками (в том числе при проверке того, есть ли эта связь вообще).

Коэффициент корреляции — числовая характеристика совместного распределения двух случайных величин, выражающая их взаимосвязь.

Существует:

• Коэффициент корреляции Пирсона;
• Коэффициенты ранговой корреляции Спирмена
• Коэффициент ранговой корреляции Кендалла
• Коэффициент конкордации.
  Коэффициент взаимной сопряженности Пирсона — оценка степени тесноты связи между качественными, но не альтернативными признаками.

Коэффициент корреляции рангов Спирмэна — непараметрическая оценка, позволяющая измерить тесноту связи как между количественными, так и между качественными признаками.

Коэффициент ранговой корреляции Спирмена. Формула расчета его имеет следующий вид:

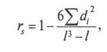
где dj – разность рангов; /– общее число сопоставляемых пар.

Коэффициент ранговой корреляции показывает, насколько одинаковыми или различными оказываются ответы на один и тот же вопрос со стороны двух сравниваемых между собою групп респондентов.

Коэффициент корреляции Кенделла – мера линейной связи между случайными величинами. Корреляция Кенделла является ранговой, то есть для оценки силы связи используются не численные значения, а соответствующие им ранги. Коэффициента корреляции Кенделла лежит в диапазоне . Применяется для выявления взаимосвязи между количественными или качественными показателями, если их можно ранжировать.

Статистические методы применяются при обработке материалов социологических исследований для того, чтобы извлечь из тех количественных данных, которые получены в экспериментах, при опросе и наблюдениях, возможно больше полезной информации.

Основной коэффициент корреляции Пирсона предназначен для оценки связи между двумя переменными, измеренными по метрической шкале, распределение которых соответствует нормальному (однако формула величины r дает достаточно точные результаты и в случаях аномальных распределений, а также в случаях, когда одна из переменных является дискретной).

Для распределений, считающихся нормальными, предпочтительнее пользоваться ранговыми коэффициентами корреляции Спирмена или Кенделла. Коэффициент корреляции изменяется на отрезке от –1 до +1.

Если между переменными существует сильная положительная связь, то значение r будет близко к +1. Если между переменными существует сильная отрицательная связь, то значение r будет близко к –1.  Когда между переменными нет линейной связи или она очень слабая, значение r будет близко к 0.

Коэффициент корреляции Пирсона является мерой прямолинейной связи между переменными: его значения достигают максимума, когда точки на графике двумерного рассеивания лежат на одной прямой. Отношения между переменными часто оказываются не только вероятностными, но и непрямолинейными: монотонными или немонотонными. Если связь нелинейная, но монотонная, то вместо r Пирсона следует использовать ранговые корреляции Спирмена или Кенделла. Ранговыми они являются потому, что сравниваемые переменные предварительно ранжируют.

Оценка значимости: уровень значимости является мерой статистической достоверности результата вычисления, в случае с корреляцией служит основанием для интерпретации. Если исследование показало, что уровень значимости не превышает 0,05, то это значит, что с вероятностью 5% и менее корреляция является случайной. Обычно это является основанием для вывода о статистической достоверности корреляции. В противном случае (p>0,05) связь признается статистически недостоверной и не подлежит содержательной интерпретации.

Коэффициенты связи, основанные на критерии хи-квадрат.

Приведем простой пример, иллюстрирующий рассматриваемый подход к пониманию связи между двумя номинальными признаками. Предположим, что перед нами стоит задача оценки того, зависит ли профессия респондента от его пола. Пусть наша анкета содержит соответствующие вопросы и в ней перечисляются пять вариантов профессий, закодированных цифрами от 1 до 5; для обозначения же мужчин и женщин используются коды 1 и 2 соответственно. Для краткости обозначим первый признак (т.е. признак, отвечающий вопросу о профессии респондента) через Y, а второй (отвечающий полу) - через X. Итак, наша задача состоит в том, чтобы определить, зависит ли Y от X.

Коэффициенты связи, основанные на моделях прогноза.

Включение понятия прогноза в представление о связи между номинальными признаками представляется разумным: наверное, трудно возражать против того, чтобы признаки считали связанными, если значение одного признака позволяет достаточно хорошо предсказать значение другого.

Предположим, что мы изучаем жителей некоторого крупного города N от 20 лет и старше и что нас интересует связь между признаком “возраст”, рассматриваемым нами как номинальный и дихотомическим признаком со значениями “студент” – “не студент”.

Коэффициенты связи, основанные на понятии энтропии.

Семейство коэффициентов, к рассмотрению которых мы переходим, основаны на такой модели связи, которая очень близка по своему содержательному смыслу к прогнозным моделям. В основе этих коэффициентов также лежит сравнение безусловного распределения с условными (условие – фиксация значения независимосго признака Х). Но сравнение это ведется не с точки зрения того, насколько при переходе от безусловного распределения к условным меняется качество возможного прогноза, а с точки зрения изучения изменения степени неопределенности рассматриваемых распределений. Здесь мы , как и в п. 1.3.5, вступаем в область теории информации и будем использовать ее терминологию.

В определенном смысле противоположным понятию энтропии является понятие информации, к рассмотрению которого мы переходим. Приобретение информации сопровождается уменьшением неопределенности, поэтому количество информации можно измерять количеством исчезнувшей неопределенности, т.е. степенью уменьшения энтропии.

Коэффициенты связи для четырехклеточных таблиц сопряженности.

Четырехклеточные таблицы – это частотные таблицы, построенные для двух дихотомических признаков.