Формулировка КХД (квантовая хромодинамика)

Квантовая хромодинамика начинается с того, что мы постулируем, что каждый кварк обладает новым внутренним квантовым числом, условно называемым цветовым зарядом, или просто цветом. Термин «цвет», конечно же, не имеет никакого отношения к оптическим цветам и введён исключительно для целей популяризации. Дело в том, что инвариантная в цветовом пространстве комбинация есть сумма трёх различных цветов. Это сильно напоминает то, что сумма трёх основных оптических цветов — красного, зелёного и синего — дает белый цвет, т. е. бесцветное состояние. Именно в этом смысле базисные вектора в цветовом пространстве часто называют не первый, второй, третий, а «красный» (к), «зелёный» (з) и «синий» (с). Антикваркам соответствуют анти-цвета (ак, аз, ас), причём комбинация «цвет + антицвет» тоже бесцветна. Глюоны же в цветовом пространстве есть комбинации «цвет-антицвет», причём такие комбинации, которые не являются инвариантными относительно вращений в цветовом пространстве. Таких независимых комбинаций оказывается восемь, и выглядят они следующим образом:

к-аз, к-ас, з-ак, з-ас, с-ак, с-аз, (к-ак − з-аз)/ $\sqrt{2}$ , (к-ак + з-аз − 2с-ас)/ $\sqrt{6}$

Например, «синий» кварк может испустить «синий-антизелёный» глюон и превратиться при этом в «зелёный» кварк.

Лагранжиан КХД

Новая внутренняя степень свободы, цвет, означает, что кварковому полю приписывается определённый вектор состояния qi единичной длины в комплексном трёхмерном цветовом пространстве C(3). Вращения в цветовом пространстве C(3), т. е. линейные преобразования, сохраняющие длину, образуют группу SU(3), размерность которой равна 32-1=8.

Поскольку группа SU(3) связна, все её элементы можно получить экспоненциированием алгебры ASU(3). Следовательно, любое вращение в C(3)

можно представить в виде U = exp(icata), где 3×3 матрицы ta (a = 1 … 8) называются матрицами Гелл-Манна и образуют алгебру ASU(3). Поскольку матрицы Гелл-Манна не коммутируют друг с другом, $= i\,f^{ab}_c t^c$ , калибровочная теория, построенная на группе SU(3), является неабелевой (то есть является теорией Янга — Миллса).

Далее используется стандартный принцип калибровочной инвариантности. Рассмотрим лагранжиан свободного кваркового поля

$L = \bar{q} (i \partial_\mu \gamma^\mu - m) q\,$

Этот лагранжиан инвариантен относительно глобальных калибровочных преобразований кварковых и антикварковых полей: $q \to \exp(i c_a t^a) q,\ \bar q \to \exp(-i c_a t^a)\bar q$ , где ca не зависят от координат в обычном пространстве.

Если же потребовать инвариантность относительно локальных калибровочных преобразований (то есть при ca(xμ)), то приходится вводить вспомогательное поле $A_\mu^a$ . В результате, лагранжиан КХД, инвариантный относительно локальных калибровочных преобразований, имеет вид (суммирование по ароматам кварков также предполагается)

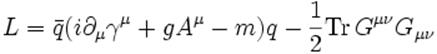
$L = \bar{q} (i \partial_\mu \gamma^\mu + g A^\mu - m)q - {1\over 2} \mathrm{Tr\,} G^{\mu\nu} G_{\mu\nu}$

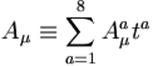где $G_{\mu\nu} = \partial_\mu A_\nu - \partial_\nu A_\mu - i g$ тензор напряжённостей глюонного поля, а $A_\mu \equiv \sum_{a=1}^{8} A^a_\mu t^a$ есть само глюонное поле.

Видно, что этот лагранжиан порождает наряду с вершиной взаимодействия кварк-антикварк-глюон и трёхглюонные и четырёхглюонные вершины. Иными словами, неабелевость теории привела к взаимодействию глюонов и к нелинейным уравнениям Янга-Миллса.

Внимание!

Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы.

Расчет стоимости Гарантии Отзывы

Поможем написать любую работу на аналогичную тему

Получить выполненную работу или консультацию специалиста по вашему учебному проекту

Узнать стоимость

Формулировка КХД (квантовая хромодинамика)

Лагранжиан КХД

Мир элементарных частиц

Фундаментальные физические взаимодействия

Гравитация

Электромагнетизм

Слабое взаимодействие

Свойства слабого взаимодействия

Сильное взаимодействие

Проблема единства физики

Классификация элементарных частиц