Экстраполяционное прогнозирование

Из формализованных методов наиболее широко применяются экстраполяционные, то есть те, когда прогноз производится по такому алгоритму:

1) упорядочение прошлых данных;
2) сглаживание временного ряда;
3) выделение тренда;
4) определение уравнения тренда;
5) расчет прогнозного значения;
6) оценка доверительного интервала с заданной вероятностью.

Наиболее простым является экстраполяция с линейным сглаживанием.

Прогнозное значение определяется подстановкой нужного значения времени в уравнение тренда y = f(t), а доверительный интервал

,

где ta — табличное значение t-критерия Стьюдента (табл. 15.1) при вероятности p и n-1 степени свободы;

n — число прошлых значений объекта прогноза, ;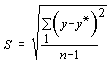
y — текущее значение объекта прогнозирования в прошлом;
y* — теоретическое значение объекта прогнозирования (исходя из уравнения тренда).

Таблица 15.1

Таблица значений t-критерия Стьюдента

Этот метод прогнозирования имеет смысл при сравнительно краткосрочном прогнозировании (5—7 лет) и уверенности в том, что основная модель процесса (а следовательно, и тренд) за это время не изменяются.

Ясно, что с целью несмещенности оценки уравнение тренда следует выбирать таким образом, чтобы S было минимальным (т.е. по методу наименьших квадратов). Практически допустимо использовать критерий

.

В том случае, если тренд целесообразно аппроксимировать монотонной произвольной кривой, целесообразно использовать преобразование масштабов осей ординат с целью "выпрямления" кривой (практически удобно преобразовывать только ось y).

Такое преобразование выполняют последовательно согласно следующей "лестнице преобразований":

.

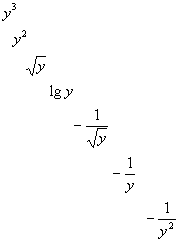Движение в ту или иную сторону по "лестнице преобразований" определяется направлением выпуклости непреобразованной кривой тренда (куда направлена, туда и надо двигаться по "лестнице"). Критерием достижения цели является равенство тангенсов углов наклона, построенных на трех характерных точках кривой (обычно начало, конец и зона изменения угла наклона). В результате получаем уравнение прямой линии преобразованной величины (например, ). Обратное преобразование дает уравнение тренда (соответственно . Далее нахождение доверительного интервала и прогнозного значения исследуемой величины осуществляется по вышеприведенным формулам.

В некоторых случаях первоначальному выделению тренда мешает неопределенность исходных данных (их "кучность" или "разреженность"). В этом случае возникает необходимость предварительного сглаживания. Наиболее прост метод сглаживания "по медианам троек". Его просто показать на примере. Предположим, есть числовой ряд:

10   1   3   5   20   7   4   10   24   25   30.

Выписываем медианы троек, последовательно передвигаясь на одно число:

3   3   5   7   7   25   25   25   30   30.

Эффект сглаживания очевиден. В целях сохранения числа данных добавляем по одному числу в начале и в конце ряда. Если полное сглаживание не достигнуто, процедура повторяется.