Поведение вещества в водной среде зависит от многих факторов:
-химических (распад, соединение с другими веществами, выпадение в осадок);
-физических (переход в другое агрегатное состояние, адсорбция, коагуляция);
-гидродинамических (перенос течениями и рассеяние в процессе турбулентной диффузии);
-биологических (аккумуляция и перенос морскими организмами).
Задачи распространения вещества в стационарном водном потоке в общем случае описываются системой дифференциальных уравнении в частных производных, включая в себя уравнение Навье-Стокса и уравнение переноса вещества, учитывающие физико-химическое взаимодействие примеси со средой и наличие источников примеси:
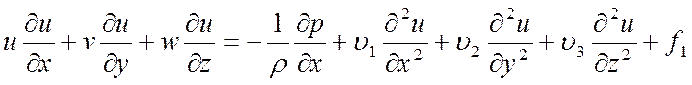
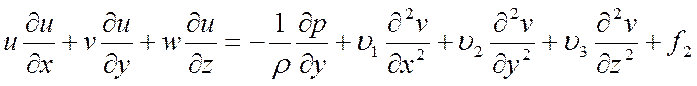
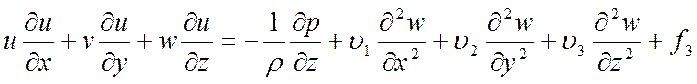
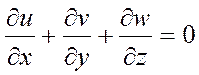- уравнение Навье-Стокса
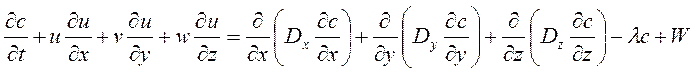
- уравнение переноса вещества.
Здесь неизвестные функции 
; 
; 
- составляющие поля скорости; 
- поле давления в стационарном потоке; 
- концентрация примеси. Известные параметры: ρ – плотность жидкости; vi – коэффициенты вязкости; fi – компоненты вектора внешней силы; λ – параметр распада веществ; W – источник загрязнений. Коэффициенты диффузии – параметры Dx, Dy, Dz – для упрощения задачи полагаются постоянными.
Для системы ставятся соответствующие краевые и начальные условия. Как правило, это условие равенства нулю скорости на твердых стенках и условия для свободной поверхности, расход воды или градиент давления, условия на поток примеси через границу, начальное распределение вещества.
Строго говоря, параметры гидродинамической подсистемы (плотность жидкости, её вязкость) должны зависеть от концентрации примеси. Однако в большинстве случаев, с целью упрощения модели, этой зависимостью пренебрегают, т.е. примесь считается пассивной. В моделях, где концентрация примеси относительно мала (в большинстве задач водной экологии оказывается именно так), такое упрощение весьма оправдано. При таком предположении гидродинамическую подсистему моно решать независимо от уравнения для концентрации.
Поможем написать любую работу на аналогичную тему