В таких задачах требуется формировать материальные потоки Xik , которыи обеспечивали бы минимальные расходы, связанные с товародвижением или максимальной прибылью предприятия, связанной с доставкой необходимых материалов.
В общем виде математическая модель системы распределения может быть сформирована в следующем виде:
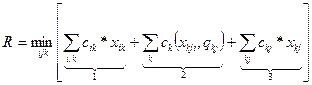
(8.1)
cik и ckj – соответствующие затраты, отнесенные к единице груза, соответствующей корреспонденции.
сk-затраты по обслуживанию материального потока в региональном распределительном центре.
Слагаемые формулы 8.1 обозначены скобками. Цифры, соответствующие каждой из скобок обозначают следующее:
1- затраты по доставке материального потока xik в региональный центр;
2- затраты, связанные с обслуживанием материальных потоков в региональном центре. Они включают расходы на хранение, информационное обеспечение, вызванные простоем вагонов под грузовыми операциями, время на выполнение грузовых операций.
3- Расходы по доставке сформированных партий из региональных центров потребителям.
Более подробно рассмотрим структуру затрат в региональном центре.
Она включает:
- расходы, связанные с хранением
,где
- стоимость хранения 1тонны груза на складе;
qkj -величина партии;
- информационные расходы
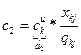, где
- стоимость передачи информации, упаковка, транспортирование.
- Расходы, вызванные простоем вагонов под грузовыми операциями
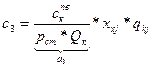, где
- стоимость приведенного вагоночаса;
рст.- статическая нагрузка вагона;
qk - перерабатывающая способность к-го распределительного центра в т/час.
- расходы связанные с выполнением грузовых операций
,где
kq- коэффициент, учитывающий число операций, выполняемых с материальным потоком.
Если kq =1.35, то это значит, что 35% грузов прошли 2 операции.
- расходы, связанные с переработкой 1единицы груза.
Учитывая принятые обозначения для с1 и с4 внесем изменения в формулу (8.1.)
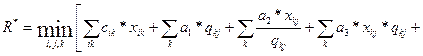
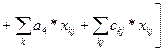(8.2)
На целевую функцию 8.2. накладываются следующие ограничения:
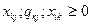;- Сумма всех материальных потоков от i-ых поставщиков в k-ый распределительный центр не должна превышать имеющийся общий ресурс.
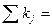pj ,где
pj-потребность каждого потребителя.
dk- перерабатывающая способность к-го распределительного центра.
Приведенная экономико-математическая модель представляет собой нелинейную функцию, которая может быть решена лишь с применением специальных методов: перебора вариантов или др.
Решение данной задачи должно быть выполнено также на основе декомпозиции, т.е. решения нескольких задач. Например:
1 задача связана с определением затрат на перемещение материального потока до к-ых распределительных центров.
2 задача: определение затрат на формирование транспортных партий груза размером qkj и перемещение этих партий с k-ых складов j-ым потребителям.
Подобного рода модели можно использовать при формировании логистических систем и определении пунктов распределения замещения региональных центров.
При этом должны учитываться как расходы, связанные с содержанием каждого регионального распределительного центра, так и транспортные расходы и инвестиции в каждый распределительный центр.
Поможем написать любую работу на аналогичную тему