Многократные равноточные измерения

Если не имеется оснований полагать, что случайные составляющие малы по сравнению с систематическими составляющими погрешностей, то ими пренебрегать нельзя. В этом случае для определения характеристик погрешностей измерений, наряду с определением систематических составляющих погрешностей, необходимо проводить многократные измерения измеряемой физической величины для определения случайных составляющих.

При многократных измерениях отдельное измерение принято называть наблюдением, и, соответственно, результат отдельного измерения при проведении многократных измерений называется результатом наблюдения.

Многократные измерения показывают, что результаты отдельных наблюдений отличаются друг от друга. Отличия наблюдаются также в результатах отдельных серий многократных измерений. В метрологии принято различать равноточные и неравноточные измерения.

К равноточным (равнорассеянным) относятся измерения, проводимые одним наблюдателем, в одинаковых условиях, с помощью одного и того же средства измерения. Равноточность выполняется при условии, что измерения являются независимыми, одинаково распределенными.

Очевидно, что при многократных измерениях не имеется возможности проведения бесконечно большого количества наблюдений, следовательно, не имеется возможности принятия в качестве результата измерения  истинного значения измеряемой величины и в качестве характеристик случайных величин принимаются не истинные, а приближенные оценки этих характеристик. Значения измеренной величины и оценок ее характеристик, в отличие от самих характеристик, являются случайными величинами, зависящими от количества проведенных наблюдений.

При многократных измерениях с ограниченным числом наблюдений (n£ £ 15) и невозможности оценить и исключить систематические погрешности ограничиваются вычислением среднего арифметического и оценки его среднего квадратического отклонения. Результат записывается в виде Хср,  sср, где sср - среднее квадратическое отклонение результата измерения.

При многократных измерениях используется методика обработки результатов наблюдений, состоящая из нескольких этапов. Ниже приведены основные этапы обработки.

1. Определяют и исключают из результатов наблюдений известные систематические погрешности:

Хi = Xi неиспр - Dсi,

где Хi  - исправленный результат отдельного наблюдения; Xi неиспр - неисправленный результат отдельного наблюдения; Dсi - систематическая погрешность отдельного наблюдения.

Как уже отмечалось, определение систематической погрешности во многих случаях является непростой задачей. Неоднократным повторением наблюдения одной и той же величины систематическую составляющую погрешности выявить невозможно, так как разброс результатов наблюдений является следствием влияния случайной составляющей погрешности. Для количественной оценки систематических погрешностей необходимы либо априорные знания об их свойствах, либо экспериментальное их определение с учетом влияющих величин. Или же требуется проведение измерений методом их сличения с использованием средств измерений более высокого класса точности.

         Чтобы эмпирически определить систематическую погрешность, требуется выявить все источники погрешностей, определить их отдельные значения. Для их оценки необходимо знать свойства используемых средств измерений, метод измерения, условия проведения измерения. Все найденные составляющие систематической погрешности суммируются.

Однако следует учитывать, что даже после определения систематической погрешности и внесения поправок в результаты наблюдений имеются неисключенные остатки систематической погрешности. Это связано с тем, что определение поправок либо поправочных множителей, а также сам процесс внесения поправок  проводится с определенной погрешностью.

При дальнейшей обработке к неисключенным остаткам систематической погрешности относятся как к случайным величинам.

         2. Вычисляют среднее арифметическое значение Хср  исправленных результатов группы наблюдений, принимаемое в качестве результата измерения:

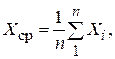                                                (6.14)

n - количество наблюдений; Хi - результат отдельного наблюдения.

Вычисленное по формуле (6.1) среднее арифметическое значение Хср является состоятельной, несмещенной и эффективной оценкой математического ожидания М при нормальном законе распределения результатов наблюдений. При любых других симметричных относительно М законах распределения Хср является состоятельной и несмещенной его  оценкой.

                Если известно, что систематическая погрешность всех наблюдений постоянна, то удобнее сначала вычислить среднее арифметическое значение  неисправленных наблюдений, а затем вычесть из него значение систематической погрешности:

Хср  = Хср неиспр - Dс ,                                           (6.15)

                                       где 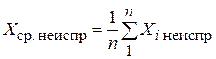 .                              (6.16)

3. Рассеивание отдельных наблюдений относительно среднего значения оценивается по среднему квадратическому отклонению результатов наблюдений.

Если проводят измерения известной величины (эталона), то в качестве эффективной оценки применяют среднюю квадратическую погрешность результатов наблюдения s*, рассчитываемую от этой известной величины (действительного значения Хд):

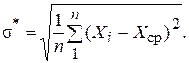(6.17)

Если измеряют неизвестную величину, то используют оценку среднеквадратического отклонения результата наблюдения s, найденную по эмпирической формуле

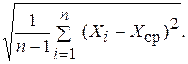
                        s =                                        (6.18)

Оценка s является несмещенной и состоятельной.

Рекомендуется провести проверку выполнения условия

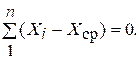
При небольшом числе наблюдений (4-10) их рассеивание можно характеризовать размахом R = Хmax - Xmin , где Хmax  и  Хmin - максимальное и минимальное значения из ряда наблюдений.

Если имеется основание считать, что в результатах наблюдений могут быть грубые погрешности, необходимо произвести проверку на их наличие.

         Результаты наблюдений, вызывающие сомнение своим отличием от остальных в большую или в меньшую сторону, необходимо проверить на отсутствие промахов при их получении. Если наличие промахов не было выявлено, необходимо произвести проверку на наличие грубой погрешности.

 Вопрос о том, содержит ли результат данного наблюдения грубую погрешность при заданной вероятности Р, можно решить с использованием критерия Романовского путем определения границ интервала, вероятность выхода случайного отклонения за пределы которого весьма мала. Эти границы gr для нормально распределенных результатов наблюдений вычисляются по формуле

gr = tгs,                                                         (6.19)

где tг - коэффициент, приведенный в табл. П3 Прилож. для заданных уровней значимости q = 1 - Р и известного числа наблюдений n; s - оценка среднего квадратического отклонения результатов наблюдений.

         Если для заданной вероятности |Хi - Хср| < gг, то можно считать, что данный результат грубой погрешности не имеет. В этом случае можно продолжать расчеты согласно методике обработки многократных равноточных измерений.

Если для выделяющегося результата наблюдения значение случайного отклонения |Хi - Хср| > g г, то этот результат можно считать имеющим грубую погрешность и его следует отбросить, т.е. количество наблюдений уменьшить на единицу. В этом случае вновь необходимо повторить пункты 1, 2, 3 методики обработки результатов прямых равноточных наблюдений, считая число наблюдений равным n - 1.

При числе наблюдений от 20 до 50 можно воспользоваться критерием "трех сигм". Критерий может быть использован для результатов наблюдений, распределенных по нормальному закону. В этом случае считается, что результат с уровнем значимости q £ 0,003 маловероятен. Поэтому, если |Хi - Хср| > 3s, то такой результат наблюдения можно считать промахом и его следует отбросить. Отметим, что правило "трех сигм" достаточно жесткое, поэтому при большом количестве наблюдений коэффициент может варьироваться в зависимости от количества результатов наблюдений. Так, при количестве наблюдений от 100 до 1000 коэффициент равен 4,5.

Известны и другие критерии, например, критерий Шарлье, критерий Диксона, вариационный критерий Граббса, или критерий Шовенэ. В частности, достаточно удобно пользоваться вариационным рядом Диксона - при его использовании наблюдаются малые вероятности ошибок. Для его использования все результаты наблюдений записываются в вариационный возрастающий ряд х1, х2, х3, . . ., хn. Критерий Диксона равен отношению (хn - хn-1)/(хn - х1). Если выясняется, что критерий больше значения Zq при заданном уровне значимости q (табл. П4 Прилож.), то данный результат считается грубой погрешностью.

Пример проверки наличия грубой погрешности в результатах наблюдений. Проведены десятикратные наблюдения падения напряжения на резисторе, которые дали следующие результаты в вольтах: 1,23; 1,83; 1,36; 1,46; 1,35; 1,49; 1,12; 1,42; 1,56; 1,38. Проверить по критериям Романовского и Диксона, содержат ли результаты наблюдения грубую погрешность при вероятностях 0,9 и 0,99.

Решение. Находим среднее значение результатов наблюдения и несмещенную оценку среднего квадратического отклонения

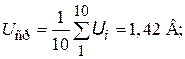
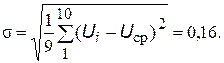
По табл. П3 Прилож. находим tг. При q = 0,1 и n = 10  tг = 2,294 при q = =0,01 и n = 10 tг = 2,616.

         Следовательно,

tгs = 2,294×0,16 = 0,37 при Р = 0,9;

tгs = 2,616×0,16 = 0,42 при Р = 0,99.

         Наиболее выделяющимся из ряда является результат второго наблюдения, поэтому произведем его проверку. Рассчитаем его разность со средним значением

|U2 - Uср| = 0,41.

         В связи с тем, что 0,41 > 0,37 при вероятности 0,9, по критерию Романовского можно сделать вывод о том, что U2 - грубая погрешность и этот результат следует отбросить. Тем самым исключаются погрешности, вероятность появления которых меньше    10 %.

При Р = 0,99 0,41< 0,42, т.е. для вероятности появления погрешностей менее 1 % грубой погрешности не обнаружено.

Проверим выполнение требования по критерию Диксона при вероятности 90 %. Расположим результаты в виде вариационного ряда: 1,23; 1,32; 1,35; 1,36;  1,38; 1,42; 1,44; 1,46; 1,56; 1,83.

Критерий Диксона

КД = (1,83 - 1,56)/(1,83 - 1,23) = 0,27/0,6 = 0,45.

Из табл. П4 Прилож. при q = 0,10 Zq = 0,35. 0,45 > 0,35, следовательно, по этому критерию результат второго наблюдения относится к грубой погрешности при уровне значимости 0,10.

При q = 0,01 Zq = 0,53. Учитывая 0,45 < 0,53, можно считать, как и по критерию Романовского, при вероятности 99 %, что грубая погрешность в результатах наблюдений отсутствует.

4. После проверки на отсутствие грубых погрешностей вычисляют оценки среднего квадратического значения результата измерения sср:

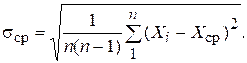
                         (6.20)

         Оценка среднего квадратического отклонения результата измерения характеризует степень рассеивания результатов отдельных наблюдений относительно среднего арифметического значения.

         Зная sср, можно найти наибольшую возможную, или предельную, погрешность Dпр. Понятие предельного значения погрешности теоретически справедливо только для погрешностей, имеющих четко выраженные границы закона распределений. Для таких законов (например, равномерного) можно указать такое значение ±Dпр, которое ограничивает возможные значения случайных погрешностей с обеих сторон от центра распределения. Для других законов распределений Dпр следует понимать как значение, выход за которое весьма маловероятен. Принято считать, что для нормального закона распределений Dпр равно 3sср, так как при нормальном законе распределения вероятность того, что результат измерения отличается от истинного не более  чем на 3sср, составляет чрезвычайно малое значение - 0,003, или 0,3 %, и такой погрешностью можно пренебречь.

         Можно определить также вероятное значение погрешности Dв, которое соответствует доверительной вероятности 0,5, а это означает, что половина погрешностей превышает Dв, а половина меньше его. Для нормального закона распределения Dв » 2/3sср.

         Недостатком оценок в виде предельных и вероятных значений является то, что они не содержат информации о характере законов распределений случайных погрешностей. Например, при арифметическом суммировании предельных погрешностей получаемая сумма может значительно превысить действительные погрешности.

         5. Проверяют гипотезу о том, что результаты наблюдений принадлежат нормальному распределению (при n > 15) - см. главу 7.

         6. Находят границы доверительного интервала случайной погрешности результата измерения D1 и D2.

         Если закон распределения неизвестен, но известны его числовые характеристики, можно грубо оценить его доверительную вероятность снизу при заданном симметричном доверительном интервале e. Для этого можно воспользоваться неравенством Чебышева:

Р ³ 1 -                                                          (6.21)

Данный способ расчета используется редко и в основном для ориентировочных оценок, так как при заданном доверительном интервале получаемое значение Р сильно занижено.

Более приближенные к действительным значения дает метод определения погрешности при законе, близком к нормальному. В этом случае используется формула

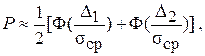
                                                                     (6.22)

где Ф(t) - интеграл  вероятности  (табл. П5 Прилож.); t1=      .

Причем Ф(-t) = -Ф(t). При симметричном доверительном интервале (D1=  =D2 = e) формула (6.9) упрощается:

                                                                                                             (6.23)

         Этот способ основан на использовании центральной предельной теоремы теории вероятности, согласно которой закон распределения суммы одинаково распределенных независимых случайных величин приближается к нормальному при условии, что число слагаемых в сумме неограниченно возрастает. Поэтому способ справедлив для любых законов распределения результатов наблюдений. Следовательно, при достаточно большом числе наблюдений (реально более 10-20) закон распределения может считаться близким к нормальному. Для малого числа наблюдений этот способ может привести к значительным ошибкам при определении доверительной вероятности.

Вероятность того, что случайная погрешность окажется за пределами интервала ± e, оценивается уровнем значимости q = 1 - Ф(t).

         Для точного определения доверительной вероятности при малом количестве наблюдений существует способ, используемый для нормального закона распределения случайных погрешностей.

         При заданном доверительном интервале доверительная вероятность может быть найдена по формуле

(6.24)                   

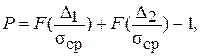
где  F(t) - функция аспределения Стьюдента

         Для симметричного доверительного интервала

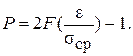
         Если требуется определить доверительный интервал, при заданной доверительной вероятности удобно воспользоваться следующими формулами:

e = tsср,  или   e* = ts*ср,                                                         (6.25)

где e - границы симметричного доверительного интервала (e = D1 = D2); t находится с использованием коэффициентов Стьюдента  при известном количестве наблюдений n.

         Использование последнего способа правомерно, если априорно известно, что закон распределения результатов отдельных независимых наблюдений нормальный либо проверка на нормальность распределения (см. главу 7) дала положительные результаты.

         При решении задач часто доверительный интервал задается в виде ±3sср, при котором доверительная вероятность составляет 0,9973, или 99,73 %. Это означает, что на 370 проведенных наблюдений допустимо одно наблюдение с результатом, выходящим за пределы ±3sср. Если сузить границы доверительного интервала до ±2sср, то доверительная вероятность составит 0,955, или 95,5 %. Тогда выход за установленные пределы допускается на каждые 22 наблюдения.

         Иногда требуется решение и обратной задачи - по заданной доверительной вероятности найти границы доверительного интервала, что возможно для всех трех способов при условии, что известны результаты отдельных наблюдений либо известна средняя квадратическая погрешность результата измерения. Если заранее доверительная вероятность не задана, то рекомендуется при технических измерениях принимать ее равной 0,95, а в особо ответственных случаях, связанных со здоровьем и безопасностью людей, применять доверительную вероятность, равную 0,99.

Пример расчета доверительной вероятности. При проведении многократных наблюдений выяснилось, что среднее квадратическое отклонение результата измерения равно 0,1 %. Считая, что границы доверительного интервала находятся в диапазоне 0,175 % от измеренного значения, рассчитать доверительную вероятность нахождения случайной погрешности в этом интервале.

Решение. Так как закон распределения погрешностей не задан, будем считать его близким к нормальному.

Из условия задачи следует, что границы симметричного интервала e равны 0,00175, sср = 0,001, отсюда t = 0,00175/0,001 = 1,75. По табл. П5 Прилож. находим значение функции Ф(t) = Ф(1,75) = 0,92. Следовательно, Р » 0,92. Уровень значимости 1 - Р » 0,08, а это значит, что лишь одна погрешность из 1250 может находиться за границами установленного доверительного интервала.