РЯДЫ ПРЕДПОЧТИТЕЛЬНЫХ ЧИСЕЛ

Высокое качество стандартов определяет высокое качество продукции. Опыт отечественной и мировой стандартизации показывает, что для обеспечения высокого качества и эффективности стандартов необходимо на стадии их разработки придерживаться ряда обязательных принципов, к числу которых относится и принцип предпочтительности.

Обычно типоразмеры деталей и типовых соединений, ряды допусков, посадок и другие параметры стандартизуют одновременно для многих отраслей промышленности, поэтому такие стандарты охватывают большой диапазон значений параметров. Чтобы повысить уровень взаимозаменяемости и уменьшить номенклатуру изделий и типоразмеров заготовок, размерного режущего инструмента, оснастки и калибров, используемых в той или иной области промышленности, а также чтобы создать условия для эффективной специализации и кооперирования заводов, удешевления продукции при унификации и разработке стандартов применяют принцип предпочтительности. Согласно этому принципу устанавливают несколько рядов (например, три) значений стандартизуемых параметров с тем, чтобы при их выборе первый ряд предпочитать второму, второй - третьему. По такому принципу построены ряды диаметров и шагов метрической резьбы, ряды нормальных углов, стандарты на допуски и посадки для гладких цилиндрических соединений и т. д. Кроме того, рекомендуется создать отраслевые ограничительные стандарты, сводящие к необходимому минимуму число допускаемых к применению параметров, типов и типоразмеров изделий.

Особо важное значение принцип предпочтительности имеет как принцип систематизации параметров и размеров машин, их частей и деталей, проводимой при унификации и стандартизации. Он основан на применении рядов предпочтительных чисел. Наиболее широко используют ряды предпочтительных чисел, построенные по геометрической прогрессии:

Un = a×Qn-1,

где а - первый член прогрессии;

Q - знаменатель прогрессии;

n = 1, 2, 3,4... - порядковый номер члена прогрессии.

Она представляет собой ряд чисел с постоянным отношением двух соседних чисел - знаменателем j прогрессии. Каждый член прогрессии является произведением предыдущего члена на j. Например, при j1 = 2 и j2 = 1,6 прогрессии соответственно имеют вид: 1; 2; 4; 8; 16; 32;... и  1; 1,6; 2,5; 4; 6,3;...Соответственно их знаменатели

j1 =;                       j2 =.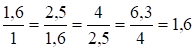

Произведение или частное любых двух членов геометрической прогрессии всегда является ее членом: 2´4=8; 8´4=32; 16:2=8; 8:2=4; 32:4=8. Любой член такой прогрессии, возведенный в целую положительную или отрицательную степень, также является членом этой прогрессии: 22=4; 23=8; 24=16; =2; =2; =4 и т. д.

В связи с перечисленными свойствами геометрической прогрессии зависимости, определяемые из произведений членов или их целых степеней, всегда подчиняются закономерности ряда. Например, если ряд определяет линейные размеры, то площади или объемы, образованные из этих линейных величин, также подчиняются его закономерности.

Наиболее удобными являются геометрические прогрессии, включающие число 1 и имеющие jn=. В соответствии с рекомендациями ИСО установлены четыре основных десятичных ряда предпочтительных чисел со знаменателями j (ГОСТ 8032-84):

=1,5849»1,6 для ряда R5;

=1,2589»1,25 для ряда R10;

=1,1220»1,12 для ряда R20;

=1,0593»1,06 для ряда R40.

В отдельных обоснованных случаях допускается применять дополнительные ряды R80 с j=»1,03, R160 с j=»1,015 и производные (выборочные) ряды, полученные из основных R5- R40 и дополнительных R80, R160 отбором каждого второго, третьего или какого-либо другого члена ряда. Можно также составлять ряды (составные ряды), которые в различных диапазонах имеют неодинаковые j. По рекомендации ИСО Р497 в науке, технике и производстве применяют округленные значения предпочтительных чисел по сравнению с числами, полученными по вышеприведенным формулам. При выборе ряда предпочтительных чисел для типоразмеров изделий целесообразно использовать ряды с большим значением j, но выбор ряда необходимо технически и экономически обосновать.

Ряды предпочтительных чисел нужно применять не только при стандартизации, но и при выборе номинальных значений параметров в процессе проектирования любых нестандартизованных машин, приборов и других изделий и их частей. Только при такой единой закономерности построения параметров и размеров изделий можно согласовать между собой параметры и размеры связанных с ними комплектующих изделий, а также полуфабрикатов и материалов.

Иногда при стандартизации применяют ряды предпочтительных чисел, построенные по арифметической прогрессии, например 1, 2, 3, 4, 5, 6,... или 25, 50, 75, 100, 125, 150,... Для арифметического ряда характерно то, что разность между любыми двумя соседними числами его всегда постоянна. Применяют также ступенчато-арифметические ряды, у которых на отдельных отрезках прогрессии разности между соседними членами различны, например ряды диаметров метрической резьбы: 1; 1,1; 1,2; 1,4; 1,6; 1,8; 2; 2,2; ... 3; 3,5; 4; 4,5; ... ; 145; 150; 155; 160 и т. д.

В радиотехнике часто применяют предпочтительные числа, построенные по рядам Е, установленным Международной электротехнической комиссией (МЭК):

ряд Е3 с j=»2,2;

ряд Е6 с j=»1,5;

ряд Е12 с j=»1,2;

ряд Е24 с j=»1,1.