На сегодняшний день в мировой практике наиболее широкое применение получили телеметрические системы контроля забойных параметров процесса бурения, в которых информация с забоя на поверхность передается гидравлическим сигналом по столбу бурового раствора. Несмотря на это необходимо отметить, что имеется весьма ограниченное число опубликованных работ, посвященных теоретическим вопросам, связанным с особенностями работы таких телесистем в реальных условиях бурения. Помимо классической книги.В. Грачева и В.II. Варламова , к таким работам следует отнести статьи Г.Д. Розенберга и И.Н. Буяновского более прикладного характера по сравнению с фундаментальной работой И.А. Чарного (имеются в виду Приложения IV и V Г.Д. Розенберга и И.Н. Буяновского в этой книге).
Почти во всех работах (за исключением работ и ) рассматривается упрощенная модель гидравлического канала в виде полубесконечной линии, в которой в качестве единственного анализируемого параметра рассматривается коэффициент затухания. Хотя затухание и имеет большое значение для анализа процессов передачи и приема гидравлических импульсов с забоя скважины на поверхность, тем не менее, такая упрошенная модель не годится для выбора оптимальных параметров передатчика и приемника сигналов, особенно для оптимальной фильтрации больших помех, имеющих место в реальных условиях бурения. С другой стороны, тот диапазон частот, в котором допущение о квазистационарности становится несправедливым (т.е. нельзя считать коэффициент затухания независимым от частоты), существенно превышает диапазон частот, в котором работают реальные системы. Приведенные в работе результаты экспериментальных исследований коэффициента затухания в гидравлическом канале связи также относятся к области высоких частот, которые на практике не применяются. Таким образом, задача анализа гидравлического канала связи, как длинной линии с распределенными параметрами, является достаточно актуальной. Для построения модели гидроканала воспользуемся дифференциальными уравнениями движения капельной сжимаемой жидкости в трубе, которые впервые были составлены и решены Н.Е. Жуковским, а затем развиты в классической работе И. А. Чарного .
В соответствии с запишем линеаризованную систему уравнений для изменений массовой скорости и давления:
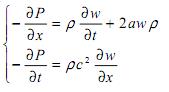 1 (1)
1 (1)
где:
P—давление в гидравлической линии:
р — плотность бурового раствора;
w — средняя скорость в сечении :
с — скорость звука в капельной упругой жидкости, текущей в трубе с упругими стенками:
а — коэффициент затухания, зависящий от кинематического коэффициента вязкости и внутреннего диаметра трубы. Для круглой трубы диаметром d имеет место равенство 2а = 32V/d2 , где V - кинематический коэффициент вязкости.
Уравнения (1) называются телеграфными, так как они встречаются в задачах распространения электрического тока вдоль кабеля.
Применение данных уравнений справедливо при условии движения жидкости со скоростью много меньше скорости звука, когда можно не учитывать изменение скоростных напоров. Скорость потока бурового раствора в канале при расходе порядка 100 л/с для бурильных труб 5" составляет примерно 11 м/с, а скорость звука в жидкости примерно равна 1500 м/с т.е. скорость потока составляет 0,7% скорости звука.
Запишем систему (1) в виде:
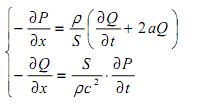
где Q = wS- объемный расход жидкости:
S- внутреннее сечение гидравлического канала (трубопровода).
Преобразуем систему (2) по Лапласу для приращений давления АР и расхода А():
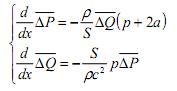 (3)
(3)
где р— переменная в преобразовании Лапласа.
Таким образом, система уравнений в частных производных (2) приведена к системе обыкновенных дифференциальных уравнений (3).
Решая систему (3), получим:
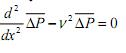 (4)
(4)
где
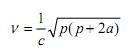 (5)
(5)
Общий интеграл решения уравнения (4) имеет вид :
![]() (6)
(6)
где А и В — произвольные константы, определяемые из граничных условий. Подставляя (6) в первое уравнение системы (3), получим выражение для приращения расхода ∆Q:
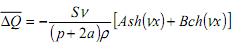
Учитывая (5) и обозначая
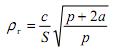
где рr - волновое сопротивление длинной линии, получим в итоге систему уравнений, определяющих с точностью до произвольных констант, преобразованные функции давления и расхода:
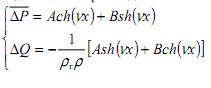
Поможем написать любую работу на аналогичную тему

