Породы коллекторы, их фильтрационные свойства

Подавляющая часть нефтяных и газовых месторождений приурочена к коллекторам трех типов – гранулярным , трещинным и смешенного строения . К первому типу относятся  коллектора, сложенные песчано – алевритовыми породами, поровое пространство которых состоит из межзерновых полостей . Подобным строение порового пространства характеризуются также некоторые пласты известняков и доломитов . В чисто трещиноватых коллекторах (сложенных преимущественно карбонатами) поровое пространство образуется системой трещин . При этом участки коллектора между трещинами представляют собой плотные малопроницаемые нетрещиноватые блоки пород, поровое пространство которых практически не участвует в процессах фильтрации .  На практике, однако, чаще всего встречаются  трещиноватые коллекторы смешанного типа , поровое пространство которых включают как системы трещин ,так и поровое пространство блоков , а также каверн и карст.

Анализ показывает , что около 60% запасов нефти в мире приурочено к песчаным пластам и песчаникам, 39%  - к карбонатным  отложениям , 1% - к выветренным метаморфическим и изверженным породам . Следовательно , породы осадочного происхождения – основные коллекторы нефти и газа .

В связи с разнообразием условий формирование осадков коллекторские   свойства пластов  различных месторождений  могут изменяться в широких пределах . Характерные особенности большинства коллекторов – слоистость и их строения и изменение во всех направлениях свойств пород, толщины пластов и других параметров .

Нефтяной пласт представляет собой горную породу , пропитанную нефтью , газом и водой .

Свойства горной породы вмещать (обусловлено пористостью горной породы)  и пропускать (обусловлено проницаемость ) через себя  жидкость называются  фильтрационно –емкостным  свойством (ФЕС) .

Фильтрационные и коллекторские свойства пород нефтяных пластов характеризуются следующими основными показателями :

– пористость;

–          проницаемость;

–          капиллярными свойствами;

–          удельной поверхностью;

–          механическими свойствами.

Под пористостью горных пород понимается наличие в ней пор (пустот). Пористость характеризует способность горной породы вмещать жидкости  и газа .         

В зависимости от происхождения различают следующие виды пор:

1. Поры между зернами обломочного материала (межкристаллические) . Это первичные поры , образовавшиеся одновременно с формированием породы .

2. Поры  растворения – образовались в  результате циркуляции подземных вод.

3. Пустоты и трещины, образованные за счёт процессов растворения минеральной составляющей породы активными флюидами и образование карста.

4. Поры и трещины, возникшие под влиянием химических процессов, например , превращение известняка (CaCO3 ) в доломит  (MgCO3 ) – при доломитизации идет сокращение объемов породы на 12%

5. Пустоты и трещины, образованные за счет выветривания , эрозионных процессов, закарстовывания.

Линейная фильтрация нефти и газа в пористой среде

Для оценки проницаемости горных пород обычно используются линейным законом фильтрации Дарси . Дарси в 1856 году, изучая течение воды через песчаный фильтр (рис. 1.6.), установил зависимость скорости фильтрации жидкости от градиента давления..

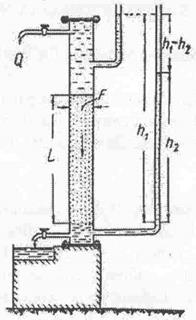
Рис. 1.6. Схема экспериментальной установки Дарси для изучения течения воды через песок

            Согласно уравнению Дарси, скорость фильтрации воды в пористой среде пропорционально градиенту давления:

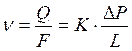                                  ,                    (1.7)

где Q – объемная скорость воды ;

       V – линейная скорость воды ;

        F – площадь сечения, F=;

        L – длина фильтра;

        k – коэффициент пропорциональности .

Нефть – неидеальная система (компонента нефти взаимодействуют между собой), поэтому линейный закон фильтрации для нефти, содержит вязкость, учитывающую взаимодействие компонентов внутри нефтяной системы:

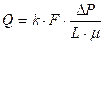                                         ,                 (1.8)

где - вязкость нефти.

В этом уравнении способность породы пропускать жидкости и газа характеризуется коэффициентом пропорциональности k (1.7.), который называется коэффициентом проницаемости ().

Размерность коэффициента проницаемости (система СИ ), вытекает из соотношении

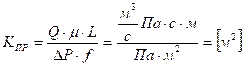,                                                   ( 1.9)

Размерность параметров уравнения Дарси в разных системах единиц

Таблица 1.2

            В системе СИ коэффициент проницаемости измеряется в м2 ; в системе СГС            =см2; в системе НПГ (нефтепромысловой геологии )  =Д (Дарси).

            1 Дарси = -8 см2=1,02.10-12м2  1мкм2.

            Проницаемость в 1м2  называется проницаемость пористой среды при фильтрации через образец площадью 1м2 длиной 1м и при перепаде давления 1 Па , при которой расход жидкости вязкостью 1 Па , с составляет  1м3.

            Пористая среда имеет проницаемость 1 Дарси, если при однофазной фильтрации жидкости вязкостью 1псз (спуаз) при ламинарном режиме фильтрации через сечение образца площадью 1 см2 и перепаде давления 1 атм., расход жидкости  на 1см длины породы составляет 1см3/ сек.

            Физический смысл размерности проницаемости  - это площадь сечения каналов пористой среды, через которые идет фильтрация .

            Существует несколько типов каналов :

-          субкапиллярный ;

-          капиллярные ;

-          трещины ;

-          разрывы ;

Приведенные выше уравнения справедливы при условии движения несжимаемой жидкости по линейному закону Дарси.

В случае фильтрации газа это условие не выполняется. При перепаде давления объем газа изменяется, и оценивается по закону Бойля – Мариотта:

           При Т=const, P.V=const                                                                      (1.10)

             При линейной фильтрации газа оценивается средняя скорость фильтрации (Vср):

                Vср. Pср = V0 . P0 = V1. P1 = V2. P2                                                                            (1.11)

                           PСР = (P1 + P2) /2 ,                                                                                                   (1.12)

Vср = V0. P0 / Pср =2. V0.P0 / (P1 + P1).                                                                                              (1.13)

Тогда, средний объемный расход газа будет равен :

.                                                                             (1.14)

Отсюда уравнение коэффициента проницаемости для газа :

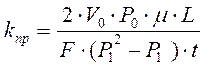                                                             (1.15)

Радиальная фильтрация нефти и газа в пористой среде

Процесс притока пластовых флюидов из пласта в скважину описывается моделью радиальной фильтрации. В этом случае образец породы представляется в виде цилиндрического кольца с проводящими каналами в осевом направлении (рис.1.7).

                                                                                          скважина

нефтяной пласт

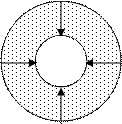Рис .1.7. схема радиального притока жидкости в скважину

            Площадь боковой поверхности цилиндра:  таким образом уравнение Дарси для радиальной фильтрации будет иметь следующий вид:

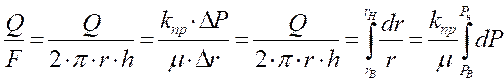.          (1.16)

Отсюда, дебит при радиальной фильтрации жидкости:

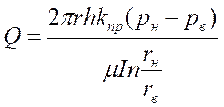 .                                                                   (1.17)           

Таким образом, коэффициент проницаемости при радиальной фильтрации:

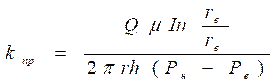.                                                        (1.18)