Определение экономического размера заказа. Экономическим размером заказа является величина партии материалов, которая позволит сократить до минимума ежегодную общую сумму затрат на запасы при определенных условиях их формирования, ценах на материалы и налогах. Методика определения экономического размера партии заключается в сравнении преимуществ и недостатков приобретения материалов большими или малыми партиями и в выборе размера заказа, соответствующего минимальной величине общих затрат на пополнение запасов. Соотношение между размером партии заказа и расходами на закупку и хранение материалов показано на рис. .
 |
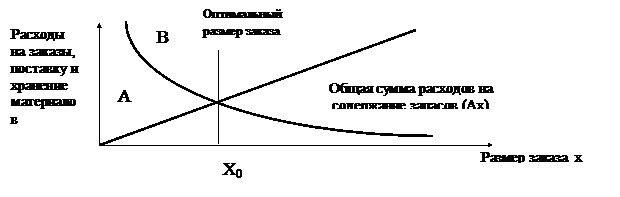Рис. . Соотношение между расходами на оформление заказа и содержание запасов и размеров заказа х
Пусть х - число единиц, закупаемых в результате одного заказа. По мере того, как возрастает число закупаемых единиц материала, текущие расходы на содержание запасов увеличиваются (кривая А). Одновременно с этим, при увеличении размера партии, количество заказов в год снижается. Это приводит к уменьшению затрат, связанных с оформлением заказов (кривая В). Покажем данную зависимость на примере.
Как видно из рис. , кривая общих годовых издержек имеет минимум при х = х0.
ПРИМЕР.
Пусть годовая потребность в материалах составляет 500 ед. И выполняется только один заказ. В этом случае запас материалов на протяжении года постепенно уменьшается с 500 ед. до нуля, что приблизительно соответствует средним запасам на уровне 250 ед. Текущие расходы на содержание запасов определяются из расчета их средней величины, а расходы на оформление заказа возникают один раз в год.
На основе количественной оценки зависимостей расходов на закупку и хранение материалов от количества закупаемого материала можно определить размер заказа, минимизирующий величину общих издержек при следующих допущениях:
1. Общее число единиц, материала составляющих годовые запасы известно.
2. Величина спроса неизменна.
3. Выполнение заказов происходит немедленно, т. е. заказы выполняют в установленные сроки, время опережения известно и постоянно.
4. Расходы на оформление не зависят от их размера.
5. Цена на материал не изменяется в течение рассматриваемого периода времени.
В соответствии с принятыми допущениями затраты на создание и содержание запасов могут быть выражены формулой
С = С1n + С2 × q/2 ,
где С1 и С2 - соответственно постоянные и переменные расходы, связанные с заказом и хранением материалов; n - количество заказов в год; q/2 - средний размер запаса.
ПРИМЕР.
Примем следующие значения затрат: С1 - затраты на поставку единицы материалов - 8,33 ден. ед./ед.; С2 - годовые затраты на содержание запасов - 0,1 ден. ед./ед. Годовая потребность в материале Q = 1500 ед. Тогда экономический размер заказа составляет
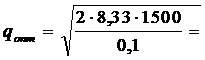500 ед.
Это означает, что ежегодно число заказов материалов n = 3 (1500/500). Поскольку спрос предполагается постоянным в течение года, заказ должен размещаться каждые 80 (240/3) рабочих дней в году.
Из рис. видно, что оптимальный размер партии находится в той области кривой суммарных затрат, которая имеет относительно пологий характер. Фактически суммарные издержки изменяются следующим образом: при размере заказываемой партии 400 ед. они составляют 51,24 ден. ед.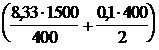 
, при 500 ед. - 50,00 ден. ед., при 600 ед. - 50,83 ден. ед. и при 700 ед. - 52,86 ден. ед. Из приведенных данных следует, что при возрастании размера партии на 40 % 
по сравнению с его оптимальной величиной, наблюдается незначительный рост суммарных издержек, всего на 5,72 % 
.
Приведенная формула устанавливает экономичный размер партии для условий равномерного и строго определенного (детерминированного) потребления запасов. В практике работы предприятия могут иметь место некоторые частные отклонения от этих условий:
1) затянувшаяся поставка. В этом случае материал поступает в течение определенного периода времени и частью используется до того, как доставлена последняя партия.
2) ускоренное использование. Это означает, что интенсивность потребления запасов такова, что возникает определенный дефицит материала.
С учетом отмеченных специальных условий строят частные модели по определению оптимальной партии заказа.
Определение оптимального размера партии. Если предприятие является своим собственным поставщиком, то формулируется задача определения оптимального размера партии, т. е. того количества продукции, которое должно быть изготовлено для пополнения запасов собственных комплектующих. Схема движения материалов, характерная для данного случая показана на рис. .
Как видно из схемы (рис. ), пополнение запаса происходит в каждом цикле за время t1, а потребление в течение всего цикла t постепенно. Необходимые комплектующие начинают изготавливать при поступлении соответствующего заказа и по мере готовности сразу же направляют потребителю: в склад цеха - получателя для дальнейшей обработки или в комплектовочный склад сборочного цеха. Дневная скорость пополнения запасов определяется из условия
(p - Q) / 240,
где р - годовой объем производства комплектующих.
Если установлены темпы производства (поступления) и потребления материалов, то запасы будут расти в течение всего периода пополнения и достигнут максимальной величины в конце этого периода.
Максимальный уровень запасов
q max = t1 (p - Q) / 240,
а средний запас составит
qср = (t1 / 2)(p - Q) / 240.
Учитывая, что период пополнения запасов определяется исходя из среднесуточного объема производства t1 = 240 qопт/р, суммарные годовые издержки, связанные с пополнением и хранением материалов составят
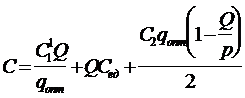
где 
- затраты на подготовку производства (они в значительной степени определяют расходы, связанные с оформлением и выдачей заказов), Cед.- себестоимость единицы продукции. Решая данное уравнение относительно qопт, получим оптимальный объем партии производства
.
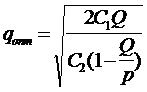Если разность между Q и p близка к нулю, то qопт приближается к бесконечности. Это означает, что в случае, когда уровень спроса равняется объему производства, производственный процесс должен быть непрерывным. Если р много больше Q, то оптимальный размер партии равен оптимальному размеру заказа и пополнение запасов возможно по первому требованию.
ПРИМЕР.
Предположим, что деталь производится на предприятии и затраты на подготовку производства равны 8,33 ден. ед. /ед. Годовое потребление деталей составляет 1500 ед., затраты на содержание единицы запаса 0,1 ден. ед., а объем годового выпуска продукции - 12000 ед. Обратим внимание, что перечисленные исходные данные нами использовались ранее в примере 5. Оптимальный размер производственной партии составит
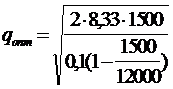= 535 ед.
Период пополнения запасов будет равен
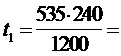11 ед.
общее время цикла
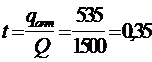или 0,35 ×240 = 84 дня.
 |
Определение оптимального размера заказа при условии оптовой скидки. Если предоставляется оптовая скидка, то для определения действительного размера заказа приходится делать несколько расчетов, так как функция суммарных издержек перестает быть непрерывной. Для нахождения глобального минимума такой функции необходимо исследовать ее локальные минимумы, причем некоторые из них могут оказаться в точках разрыва цен.
ПРИМЕР.
Предположим, что поставщик предложил следующие цены, учитывающие скидки за количество:
Цена, ден. ед. Размер заказа
2,00 0 - 9999
1,60 10000 - 19999
1,40 20000 и более.
Удельные затраты потребителя на содержание запасов соответственно равны 0,4 ден. ед., 0,32 ден. ед. И 0,28 ден. ед. Годовое потребление 1000000 ед. и затраты на поставку 28,8 ден. ед.
Оптимальный размер заказа без учета скидок при цене 2,00 ден. ед. равен
= 
= 12000 ед.
Если дается 20 % скидка и установлена цена в 1,6 ден. ед.
= 
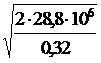= 13416 ед.
При цене 1,4 ден. ед. получим
= 
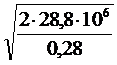= 14350 ед.
Мы нашли, что для цены 1,6 ден. ед. Размер заказа 
= 13416 ед. с учетом полученных данных, рассчитаем суммарные годовые издержки
С = 
1604293,12 ден. ед.
Для нахождения общих годовых затрат при цене 1,40 ден. ед. И предложенной структуре оптовых скидок к цене мы должны использовать минимальный объем партии в 20000 ед., а не величину 
= 14350 ед., рассчитанную выше. Для этого случая суммарные годовые затраты будут составлять
С = 
1404240,00 ден. ед.
Из приведенных расчетов можно сделать вывод, что целесообразны закупки партиями по 20000 ед. Покупать большими или меньшими партиями будет менее выгодно.
Кривая суммарных годовых затрат для рассмотренного примера приведена на рис. (график сделан не в масштабе, но отражает вид зависимости, характерной для данного примера).
Определение оптимального размера заказа при допущении дефицита. В классической модели экономичного размера заказа дефицит продукции, необходимой для производства, не предусмотрен. Однако в случаях, когда потери из-за дефицита сравнимы с издержками по содержанию излишних запасов, дефицит допустим. При наличии его модель оптимального размера партии требует учета определенных методических особенностей. Наиболее общий случай движения текущего, запаса при допущении дефицита материала представлен на рис. 20, где qn - размер запаса в начале каждого интервала между поставками t (максимальный запас при дефиците). Весь интервал t делится на два периода:
а) время, в течение которого запас на складе имеется в наличии, t1;
б) время, в течение которого запас отсутствует, t2. Начальный размер запаса qn в этих условиях принят несколько меньше, чем оптимальный размер партии qопт. Задача управления запасами сводится к количественному определению размера снижения и установлению наиболее рациональной величины начального запаса. Критерием оптимальности партии поставки является минимальная сумма транспортно-заготовительных расходов, расходов на содержание запаса и убытка от дефицита.
.
,
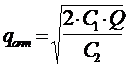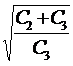где С3 потери из-за дефицита продукции в год.
При значительном увеличении С3 отношение С3/(С2 + С3) приближается к 1 и оптимальный размер партий стремится к значению, которое было бы при отсутствии дефицита запасов. Если потери из-за дефицита очень малы, то отношение С3/(С2 + С3) стремится к нулю, а оптимальный размер партии к бесконечности, т. е. допускается большой дефицит запасов.
ПРИМЕР.
Пусть оптимальный размер партии деталей х равен 500 ед. И потери от дефицита составляют 0,20 ден. ед. в год. Находим
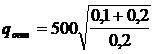= 613,
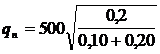= 408.
Общее время цикла
Т = 
= 0,41 или 0,41 . 240 = 98,4 дня.
Приведенные расчеты показывают, что в том случае, когда допускается дефицит, имеет место большая величина оптимального размера заказа (613 ед. Вместо 500 ед.) и большое время цикла между точками заказов (0,41 года вместо 0,33 года).
Поможем написать любую работу на аналогичную тему