Основные понятия и принципы синергетики

Порядок и хаос. В результате протекания процессов в изолированных системах сами системы переходят в состояние равновесия, которое соответствует максимальному беспорядку системы – равновесный тепловой хаос. Таким образом, самоорганизация, или эволюция в случае замкнутой системы приводит ее в состояние максимального беспорядка. В реальности, тем не менее, часто наблюдаются совершенно противоположные явления.

Уже теория Канта и Лапласа об образовании упорядоченной Солнечной системы из хаотических туманностей противоречила II началу термодинамики. Но особенно ярко проявилось противоречие II начала термодинамики с эволюционной теорией Дарвина. Ведь согласно ей, в мире живого естественно протекающие процессы ведут к усложнению форм и структур, к увеличению порядка, избавлению от хаоса и удалению от равновесия. Другими словами, самоорганизация в живой природе приводит систему к прямо противоположному состоянию, чем самоорганизация в неживых системах. Все это привело к появлению понятия открытой системы, которое и позволило устранить упомянутые противоречия.

Открытость систем.  Такие понятия как изолированная (закрытая) система, необратимые процессы являются идеализацией. При изучении обратимых процессов (например, качание маятника в вакууме при отсутствии трения) нет смысла говорить о направлении течения времени, т.к. прошлое, настоящее и будущее в этом случае не отличаются. Поэтому в уравнениях обратимых процессов время выступает всего лишь как параметр, который можно изменять. Но в реальности в случае с маятником всегда присутствует трение, колебания маятника будут затухающими, и прошлое, настоящее и будущее будут уже отличаться. Ранее уже говорилось о том, что необратимых процессов в живой природе эволюционным принципом стало II начало термодинамики, утверждающее, что энтропия изолированной системы возрастает. Именно рост энтропии устанавливает направление протекания процесса, т.е. «стрелу времени».

В своей книге «Что такое жизнь» выдающийся австрийский физик Э. Шредингер указал на то, что средство, при помощи которого организм поддерживает себя на достаточно высоком уровне упорядоченности, т.е. на достаточно низком уровне энтропии, в действительности состоит в непрерывном извлечении упорядоченности из окружающей его среды. Другими словами, организм извлекает из окружающей среды негэнтропию. Открытая система заимствует энергию и вещество из окружающей его среды и одновременно выводит в окружающую среду отработанное вещество и отработанную энергию. Вырабатывая и заимствуя энергию, открытая система производит энтропию, но она не накапливается в ней, а выводится в окружающую среду. С поступлением энергии и вещества в открытую систему ее неравновесность возрастает, разрушаются прежние связи между элементами и возникают новые, которые приводят к новой структуре, новым кооперативным процессам, т.е. к коллективному поведению ее элементов.

Нелинейность. Сложные системы являются нелинейными. Для их описания используются нелинейные математические уравнения, т.е. уравнения, в которых искомые величины входят в степенях больше единицы, в составе математических функций (тригонометрических, логарифмических и т.п.) или коэффициенты зависят от свойств среды и особенностей протекания процесса. Нелинейные уравнения могут иметь несколько качественно различных решений. Физически это означает возможность различных путей эволюции системы.

Диссипативность. Великий русский математик А.М.Ляпунов разработал общую теорию устойчивости состояний систем. Очень кратко ее идею можно выразить следующим образом. Устойчивые состояния систем не теряют своей устойчивости при флуктуациях физических параметров, поскольку система за счет внутренних взаимодействий способна погасить возникающие флуктуации. Неустойчивые системы, наоборот, при возникновении флуктуаций способны усиливать их, и, в результате такого нарастания амплитуд возмущений система уходит из стационарного состояния. Критерием эволюции при этом является величина (dS/dt) < 0, которая указывает направление развития физической системы к устойчивому стационарному состоянию. Эти процессы происходят достаточно медленно, поэтому на каждом этапе как бы достигается равновесие. Величина прироста энтропии за единицу времени в единице объема называется функцией диссипации, а системы, в которых функция диссипации отлична от нуля, называются диссипативными. В таких системах энергия упорядоченного движения переходит в энергию неупорядоченного движения и, в конечном счете, в тепло. Практически все системы являются таковыми, поскольку трение и прочие силы сопротивления приводят к диссипации энергии (диссипация < лат. dissipatio – разгонять, рассеивать).

При определенных условиях суммарное уменьшение энтропии за счет обмена потоками с внешней средой может превысить ее внутреннее производство. Тогда неупорядоченное однородное состояние системы может потерять устойчивость. В ней возникают и могут возрасти до макроскопического уровня т.н. крупномасштабные флуктуации. При этом из хаоса могут возникнуть структуры, которые последовательно начнут переходить во все более упорядоченные. Образование этих структур происходит не из=за внешнего воздействия, а за счет внутренней перестройки системы, поэтому это явление и получило название самоорганизации. При этом энтропия, отнесенная к тому же значению энергии, убывает. Пригожин назвал упорядоченные образования, возникающие в диссипативных системах в ходе неравновесных необратимых процессов, диссипативными структурами.

На макроуровне диссипативность проявляется как хаос. На микроуровне хаос – это не разрушающий фактор, а сила, выводящая систему путь образования новых структур.

Бифуркации. Выше было сказано, что нелинейная система уравнений, которой описывается практически любая реальная сложная система, имеет не одно, а подчас целый спектр решений. Ответвления от известного решения появляются при изменении значения параметров системы. Поэтому мы введем здесь еще одно понятие - управляющие параметры (параметры порядка). Изменения управляющих параметров способны вызвать катастрофические, т.е. большие скачки переменных системы, и эти скачки осуществляются практически мгновенно.

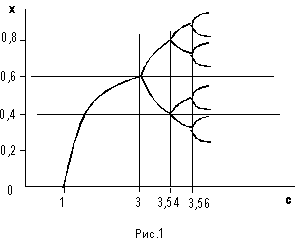
Путь на изолированном острове выводятся летом насекомые численностью xj и откладывают яйца. Потомство их на следующее лето появится численностью xj+1  =  cxj (1- xj ).  Рост популяции насекомых описывается первым членом в правой части уравнения xj, а убыль – вторым. Параметр роста (коэффициент пропорциональности) с является управляющим параметром. При с<1 популяция при увеличении j убывает и исчезает. В области 1<c<3 численность приближается к значению x = 1 - (1/c). Следующий диапазон 3<c<3,4 соответствует двум ветвям решения и при определенных условиях численность может колебаться между ними (рис. 1). Т.е. она растет резко от малого значения, и откладывается много яиц. Но перенаселенность, возникающая на следующий год, вновь снижает численность в следующем году до малого значения., так что период колебания численности равен двум годам. Далее, при 3,4<c<3,54 имеем уже 4 ветви, и возникает 4—стадийный цикл колебаний и. т.д. Подобные решения имеют место для широкого класса систем химических, электрических, гидродинамических и т.д.

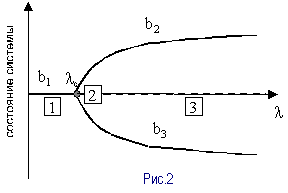
Итак, при изменении управляющих параметров в системе наблюдаются различные переходные явления, которые мы рассмотрим с помощью т.н. диаграммы бифуркации (см. рис. 2).

1 – асимптотическая ветвь, где система остается устойчивой, т.е. при малых l имеет одно единственное решение
2 – точка, где l=lС - здесь происходит потеря устойчивости. Появляется два решения.
3 – система вновь находится в равновесии, причем существуют 2 устойчивые ветви b1 и b2.

Сама точка lС носит название точки бифуркации (<лат. раздвоение, размножение) или «точкой катастрофы».

Ранее уже использовалось понятие флуктуации, т.е. отклонение какой-либо величины от среднего значения. Здесь, как видим, малая флуктуация управляющего параметра может иметь определяющее значение для системы (она начинает развиваться либо по ветви b1, либо по ветви b2). В биологической эволюции флуктуации проявляются в мутациях, изменчивости, в то время как устойчивость обусловлена естественным отбором.

Усложнение структуры и поведения системы тесно связано с появлением новых путей решения в результате бифуркаций. В сильно неравновесных условиях процессы самоорганизации соответствуют «тонкому взаимодействию» между случайностью и необходимостью, флуктуациями и детерминистскими законами. Вблизи бифуркаций, т.е. резких, «взрывных» изменений системы, основную роль играют флуктуации или случайные элементы, тогда как в интервалах между бифуркациями преобладает детерминизм. Ситуацию, возникающую после воздействия флуктуации на систему и возникновения новой структуры, И. Пригожин назвал порядком через флуктуацию или «порядком из хаоса». Флуктуации могут усиливаться в процессе эволюции системы или затухать, что зависит от эффективности «канала связи» между системой и внешним миром.

Аттракторы и фазовые траектории.  Для выяснения сущности этих понятий рассмотрим динамическую систему. Понятие динамической системы состоит из двух частей: понятия состояния (существенной информации о системе) и динамики (правила, описывающего эволюцию системы во времени). Эволюцию можно наблюдать в пространстве состояний, или фазовом пространстве, - абстрактном пространстве, в котором координатами служат компоненты состояния. При этом координаты выбираются в зависимости от контекста. В случае механической системы это могут быть положение и скорость, в случае экологической модели - популяции различных биологических видов.

Пусть интересующий нас процесс зависит только от одной переменной (например, от времени t ) и может быть смоделирован с помощью системы дифференциальных уравнений вида

   , (2.1)

где  - N- мерный вектор, характеризующий состояние системы, - начальные данные. К числу математических моделей такого рода относятся, например, уравнения механики для системы материальных точек (движение планет Солнечной системы, груза на наклонной плоскости, элементарной частицы в электромагнитном поле и др.). Число явлений окружающего мира, которое может быть описано с помощью подобных моделей огромно, однако число моделей, которые могут быть изучены путем вычислительного эксперимента на компьютерах весьма ограничено, а уравнения, которые могут быть решены аналитически, составляют чрезвычайно малую долю.

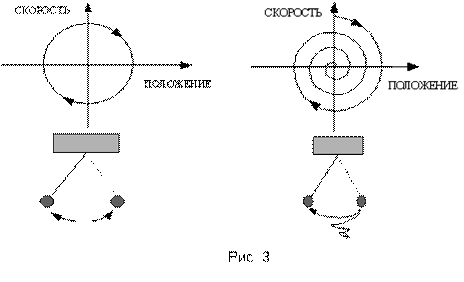
Рассмотрим наиболее простой пример динамической системы - простой маятник. Его движение задается всего двумя переменными: положением и скоростью. Таким образом, его состояние - это точка на плоскости, координаты которой - положение маятника и его скорость. Это означает, что размерность вектора, характеризующего состояние маятника N = 2. Эволюция состояния описывается правилом, которое выводится из законов Ньютона и выражается математически в виде дифференциального уравнения. Когда маятник качается взад-вперед, его состояние - точка на плоскости - движется по некоторой траектории («орбите»). В идеальном случае маятника без трения орбита представляет собой петлю; при наличии трения орбита закручивается по спирали к некоторой точке, соответствующей остановке маятника (см. рис. 3). Часы с маятником, которые заводятся при помощи пружины или гирь, также проходят циклически некоторую последовательность состояний. Маятник снова и снова повторяет свой путь. В фазовом пространстве его движению соответствует периодическая траектория, или цикл. Неважно, как маятник запущен в движение - в конце концов, он придет к тому же циклу. Такие аттракторы называются предельными циклами. Другим примером системы с предельным циклом является сердце.

Точка или множество точек (например, петля, цикл), к которому стремится прийти система, называется аттрактором (от лат. attractio – притягиваю). Другими словами, аттрактор – это точка или некоторое множество точек, к которому стремится динамическая система с течением времени, как бы «забывая» начальные условия. Действительно, каковы бы не были начальные значения переменных системы, по мере развития динамического процесса, они будут стремиться к одним и тем же значениям или одним и тем же множествам значений – аттракторам. Таким образом, аттракторы - это геометрические структуры, характеризующие поведение в фазовом пространстве по прошествии длительного времени.

Одна и та же система может иметь несколько аттракторов. Если это так, то разные начальные условия могут привести к разным аттракторам. Множество точек, приводящих к некоторому аттрактору, называется его областью притяжения. Система с маятником имеет две такие области: при небольшом смещении маятника от точки покоя он возвращается в эту точку, однако при большом отклонении часы начинают тикать, и маятник совершает стабильные колебания.

Свойства аттракторов задаются набором траекторий в пространстве n переменных состояния, которые зависят от времени как от параметра. В обычном аттракторе эти траектории простые (точка, окружность, эллипс и т.п.). Но ряд явлений сопровождается появлением траекторий запутанных, не похожих ни на точки, ни на кривые, ни на поверхности, имеют вид «спутанных клубков», многослойных поверхностей. Такие аттракторы получили названия «странных аттракторов». Странность состоит в том, что, попав в область странного аттрактора, точка, соответствующая состоянию системы будет «блуждать» там и только через большой промежуток времени приблизится к какой-либо точке аттрактора. Поведение системы выглядит при этом хаотическим, а ее дальнейшее поведение сильно зависит от начальных условий.