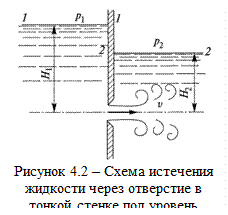
При течении жидкости в закрытых руслах часто приходится иметь дело с истечением жидкости не в газовую среду, а в пространство, заполненное этой же жидкостью (рисунок 4.2). Такое истечение называется истечением под уровень или истечением через затопленное отверстие.
Здесь, так же как и в предыдущем случае, при определении расхода Q следует составить уравнение Бернулли. Запишем его для сечений 1-1 и 2-2, в которых скорости движения жидкости принимаются равными нулю:
,
где 
— потери напора при движении жидкости между сечениями 1-1 и 2-2.
При определении потерь напора в этом случае необходимо учитывать, что они складываются из двух составляющих:
,
где ho — потери напора на торможение частиц жидкости о входную кромку отверстия;
hв.р — потери напора на внезапное расширение в баке после прохождения жидкости через отверстие.
Потери ho практически равны потерям при истечении через отверстие в газовую среду:
.
Следует иметь в виду, что при истечении под уровень вся кинетическая энергия струи, приобретенная частицами жидкости в отверстии, при попадании в покоящуюся жидкость теряется на вихреобразование так же, как при внезапном расширении. Поэтому потери hв.р численно равны соответствующему скоростному напору, посчитанному по средней скорости жидкости в струе с учетом коэффициента Кориолиса α:
.
Таким образом, суммарные потери напора
.
Подставив полученное выражение в уравнение Бернулли, получим
.
Если в этом уравнении за расчетный напор принять выражение 
, то после преобразований можно получить формулу, определяющую значение средней скорости жидкости в сжатом сечении струи:
,
которая совпадает с формулой (4.2). Это значит, что, проводя дальнейшие преобразования, необходимые для получения формулы, определяющей расход Q при истечении, можно получить формулы (4.6) и (4.7).
Таким образом, как при истечении в газовую среду, так и при истечении под уровень расчетные формулы, определяющие расход Q, имеют один и тот же вид. Кроме того, как показала практика, коэффициенты 
, 
и 
, использующиеся в этих формулах, в обоих случаях истечения имеют одинаковые значения при равенстве соответствующих чисел Рейнольдса.
Поможем написать любую работу на аналогичную тему