Местные сопротивления при больших и малых числах Рейнольдса. Метод эквивалентной длины

Ранее были рассмотрены местные гидравлические сопротивления, потери напора в которых пропорциональны квадрату скорости или расхода. Однако квадратичный характер зависимости потерь - наиболее распространенный, но все же частный случай для местного сопротивления.

В машиностроительных гидросистемах встречаются местные сопротивления, внутри которых имеет место ламинарное течение. Потери напора в таких сопротивлениях

пропорциональны скорости (или расходу) в первой степени, т.е. носят линейный характер. Кроме того, при ламинарном течении жидкости в трубах коэффициенты местных сопротивлений не всегда остаются постоянными. Указанные сопротивления встречаются существенно реже, чем сопротивления с квадратичной зависимостью потерь, и не имеют определяющего значения, но при расчете отдельных гидросистем их необходимо учитывать.

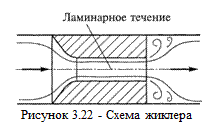
В качестве примера рассмотрим жиклер (рисунок 3.21), в канале которого существует ламинарное течение. Потери напора в жиклере будут складываться из потерь на трение в канале и потерь на внезапное расширение потока при выходе из этого канала. Причем первый вид из указанных потерь будет пропорционален скорости в первой степени (так как в канале ламинарное течение), а второй - квадрату скорости (потери на вихреобразование).

Если принимать во внимание оба вида потерь, то формула для коэффициента сопротивления жиклера будет иметь вид

.                                                    (3.38)

Это общее выражение для коэффициента любого местного сопротивления. Первое слагаемое в (3.38) учитывает линейные потери, а второе - квадратичные. Соотношение между первым и вторым слагаемыми зависит от геометрических размеров каждого конкретного сопротивления.

Использование зависимости (3.38) приводит к значительному усложнению при расчетах гидравлических систем. Однако практика показывает, что в подавляющем большинстве местных сопротивлений один из видов потерь существенно превышает второй, поэтому при проведении реальных расчетов одним из слагаемых формулы (3.38) пренебрегают.

На практике для местных сопротивлений с линейным законом сопротивления (или с законом, близким к линейному) часто применяют метод эквивалентной длины. Сущность этого метода заключается в том, что для местного сопротивления задаются эквивалентная длина и условный диаметр (или условная площадь сечения). Причем их значения выбираются такими, что потери напора в условном трубопроводе равны потерям в данном гидравлическом сопротивлении. Тогда потери в трубопроводе с таким местным сопротивлением можно рассчитать по обобщенной формуле Пуазейля

,

где lp = l +lэкв – расчетная длина трубопровода;

      l – фактическая длина;

      l’экв – эквивалентная длина.

К таким сопротивлениям относятся большинство фильтров, а также линейные дроссели и некоторые жиклеры.