Для определения λ при турбулентном режиме предложен ряд эмпирических и полуэмпирических формул, полученных многими авторами в результате исследования различных областей гидравлического трения. Однако фундаментальным исследованием стала работа И. И. Никурадзе, который в 1933 г. опубликовал результаты своих многочисленных опытов, представленных в виде особого графика.
В своих опытах Никурадзе исследовал напорное движение жидкости в круглоцилиндрических трубах, имеющих однозернистую равномерно распределенную (равнозернистую) шероховатость, которую он создавал путем наклеивания калиброванных песчинок высотой Δ на внутреннюю поверхность трубы.
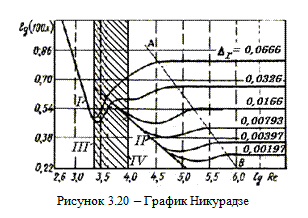
Полученный Никурадзе график представляет собой семейство кривых, построенных в логарифмических координатах (по горизонтальной оси отложены величины lg ReD, а по вертикальной — lg 100λ) по точкам, соответствующим опытам с трубами с различной относительной шероховатостью Δr = Δ : D, от Δr = 0,00197 до Δr = 0,0666.
Рассмотрим подробно график Никурадзе (рисунок 3.20). Все поле графика можно условно разбить на пять областей.
Первая область — область ламинарного режима при Re < 2300, (lg Re ≤ 3,36), здесь все опытные точки независимо от шероховатости уложились на одну прямую линию I, уравнение которой λ = 64 / Re.
Вторая область, расположенная между вертикалями III и IV, — область неустойчивого режима или переходная (числа Рейнольдса лежат в пределах от 2300 до 10000). Здесь возможно существование как ламинарного, так и турбулентного режимов, экспериментальные точки имеют значительный разброс.
Третья область — область гидравлически гладких труб» при турбулентном режиме, здесь толщина вязкого подслоя существенно больше высоты выступов шероховатости и турбулентное ядро потока не соприкасается с ними. Поэтому в этой области коэффициент λ = f (Re) не зависит от шероховатости. Область гладких труб представлена на графике прямой линией II, уравнение которой
. (3.30)
Эта эмпирическая формула была получена Блазиусом в 1913г. в результате обработки многочисленных опытов по исследованию движения жидкости в круглых гладких латунных трубах при числах Рейнольдса Re от 2300 до 100000.
Четвертая область — область турбулентного режима доквадратичного сопротивления шероховатых труб, лежит между прямой II и линией АВ, образованной точками, отделяющими горизонтальные участки кривых с некоторой заданной точностью. Можно видеть, что в этой области каждая кривая отвечает определенному значению относительной шероховатости. Здесь турбулентное ядро постепенно раскрывает шероховатость, поэтому имеет место наиболее общий случай λ = f (Re, Δr).
Пятая область — область турбулентного режима квадратичного сопротивления шероховатых труб, располагается правее и выше линий АВ. Здесь коэффициент λ не зависит от числа Рейнольдса Re (все линии графика — прямые, параллельные горизонтальной оси). Коэффициент λ, а следовательно, и потеря напора hтр зависят от шероховатости λ = f (Δr). Таким образом, как видно из формулы Вейсбаха - Дарси, для этой области сопротивления потеря напора по длине прямо пропорциональна квадрату средней скорости.
В заключение необходимо отметить, что общий качественный характер зависимостей коэффициента гидравлического трения λ, полученный Никурадзе для труб круглого сечения, распространяется и на другие потоки, в том числе и безнапорные, что было подтверждено опытами А. П. Зегжды, в которых исследовалось безнапорное движение жидкости в лотке прямоугольного сечения, имеющего различную равнозернистую шероховатость. Важно также подчеркнуть, что после указанных работ отпала необходимость создавать особые расчетные зависимости для различных жидкостей, так как род жидкости учитывается числом Рейнольдса.
Поможем написать любую работу на аналогичную тему