Соединения простых трубопроводов. Аналитические и графические способы расчета

Рассмотрим способы расчета соединений простых трубопроводов.

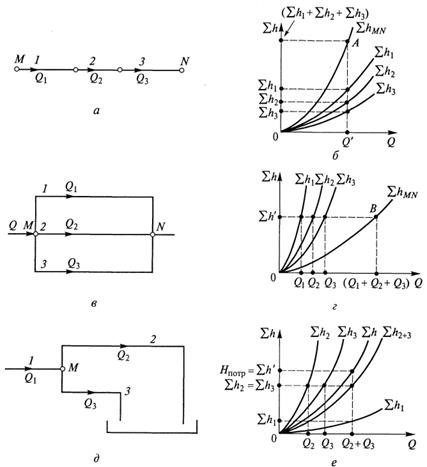
Пусть имеем последовательное соединение нескольких простых трубопроводов (1, 2 и 3 на рисунке 5.3, а) различной длины, разного диаметра, с различным набором местных сопротивлений. Так как эти трубопроводы включены последовательно, то в каждом из них имеет место один и тот же расход жидкости Q. Суммарная потеря напора для всего соединения (между точками М и N)  складывается из потерь напора в каждом простом трубопроводе (, , ), т.е. для последовательного соединения справедлива следующая система уравнений:

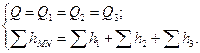                                                 (5.6)

Потери напора в каждом простом трубопроводе могут быть определены через значения соответствующих расходов:

; ; .                                           (5.7)

Система уравнений (5.6), дополненная зависимостями (5.7), является основой для аналитического расчета гидросистемы с последовательным соединением трубопроводов.

Если используется графический метод расчета, то при этом возникает необходимость в построении суммарной характеристики соединения.

На рисунке 5.3, б показан способ получения суммарной характеристики последовательного соединения. Для этого используются характеристики простых трубопроводов 1, 2 и 3, которые строятся по зависимостям (5.7).

Для построения точки, принадлежащей суммарной характеристике последовательного соединения, необходимо в соответствии с (5.6) сложить потери напора в исходных трубопроводах при одинаковом расходе. С этой целью на графике проводят произвольную вертикальную линию (при произвольном расходе Q'). По этой вертикали суммируют отрезки (потери напора ,  и ) получившиеся от пересечения вертикали с исходными характеристиками трубопроводов. Полученная таким образом точка А будет принадлежать суммарной характеристике соединения. Следовательно, суммарная характеристика последовательного соединения нескольких простых трубопроводов получается в результате сложения ординат точек исходных характеристик при данном расходе.

Параллельным называется соединение трубопроводов, имеющих две общие точки (точку разветвления и точку смыкания). Пример параллельного соединения трех простых трубопроводов приведен на рисунке 5.3, в. Очевидно, что расход Q жидкости в гидросистеме до разветвления (точка М) и после смыкания (точка N) один и тот же и равен сумме расходов Q1, Q2 и Q3 в параллельных ветвях.

Если обозначить полные напоры в точках M и N через НM и HN, то для каждого трубопровода потеря напора равна разности этих напоров:

; ; ,

т. е. в параллельных трубопроводах потери напора всегда одинаковы. Это объясняется тем, что при таком соединении, несмотря на разные гидравлические сопротивления каждого простого трубопровода, расходы Q1, Q2 и Q3 распределяются между ними так, что потери остаются равными.

Таким образом, система уравнений для параллельного соединения имеет вид

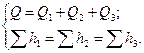                                                                (5.8)

Потери напора в каждом трубопроводе, входящем в соединение, могут быть определены по формулам вида (5.7). Таким образом, система уравнений (5.8), дополненная формулами (5.7), является основой для аналитического расчета гидросистем с параллельным соединением трубопроводов.

На рисунке 5.3, г показан способ получения суммарной характеристики параллельного соединения. Для этого используются характеристики простых трубопроводов 1, 2 и 3, которые строятся по зависимостям (5.7).

Для получения точки, принадлежащей суммарной характеристике параллельного соединения, необходимо в соответствии с (5.8) сложить расходы в исходных трубопроводах при одинаковых потерях напора. С этой целью на графике проводят произвольную горизонтальную линию (при произвольной потере ). По этой горизонтали графически суммируют отрезки (расходы Q1, Q2 и Q3), получившиеся от пересечения горизонтали с исходными характеристиками трубопроводов. Полученная таким образом точка В принадлежит суммарной характеристике соединения. Следовательно, суммарная характеристика параллельного соединения трубопроводов получается в результате сложения абсцисс точек исходных характеристик при данных потерях.

По аналогичному методу строятся суммарные характеристики для разветвленных трубопроводов. Разветвленным соединением называется совокупность нескольких трубопроводов, имеющих одну общую точку (место разветвления или смыкания труб).

Рассмотренные выше последовательное и параллельное соединения, строго говоря, относятся к разряду сложных трубопроводов. Однако в гидравлике под сложным трубопроводом, как правило, понимают соединение нескольких последовательно и параллельно включенных простых трубопроводов.

На рисунке 5.3, д приведен пример такого сложного трубопровода, состоящего из трех трубопроводов 1, 2 и 3. Трубопровод 1 включен последовательно по отношению к трубопроводам 2 и 3. Трубопроводы 2 и 3 можно считать параллельными, так как они имеют общую точку разветвления (точка М) и подают жидкость в один и тот же гидробак.

Для сложных трубопроводов расчет, как правило, проводится графическим методом. При этом рекомендуется следующая последовательность:

1) сложный трубопровод разбивается на ряд простых трубопроводов;

2) для каждого простого трубопровода строится его характеристика;

3) графическим сложением получают характеристику сложного трубопровода.

На рисунке 5.3, е показана последовательность графических построений при получении суммарной характеристики () сложного трубопровода. Вначале складываются характеристики трубопроводов  и  по правилу сложения характеристик параллельных трубопроводов, а затем характеристика  параллельного соединения складывается с характеристикой  по правилу сложения характеристик последовательно соединенных трубопроводов и получается характеристика всего сложного трубопровода .

Имея построенный таким образом график (см. рисунок 5.3, е) для сложного трубопровода, можно достаточно просто по известному значению расхода Q1, поступающего в гидросистему, определить потребный напор Hпотр =  для всего сложного трубопровода, расходы Q2 и Q3  в параллельных ветвях, а также потери напора ,  и  в каждом простом трубопроводе.