Сопротивления движению жидкости, обуславливаемые трением (вязкостью), а также изменением конфигурации потока, называются гидравлическими сопротивлениями,
Установившееся движение жидкости в потоке может быть неравномерное и равномерное
Равномерным называется вид установившегося движения, при котором элементы потока (скорости, живые сечения, глубины и пр.) не изменяются вдоль потока.
Как неравномерное, так и равномерное движение жидкости могут проявляться в двух формах: напорного и безнапорного движения.
Движение потока в трубе (водоводе) полным ее сечением, когда давление в жидкости больше атмосферного, называется напорным.
Движение потока со свободной поверхностью, давление над которой известно и одинаково на протяжении потока называется безнапорным. (Открытые русла, каналы, канализационные трубы с частичным заполнением трубы и т.д.)
Кроме известных из предыдущего элементов потока: расхода Q, средней скорости v , площади живого сечения w, следует различать еще:
- смоченный периметр - c;
- гидравлический радиус - 
;
- ширину потока на уровне свободной поверхности - B ;
- среднюю гдубину потока 
;
- гидравлический уклон потока - потеря энергии потока (напора) на единицу длины потока 
.
При равномерном напорном движении жидкости гидравлический уклон равен пьезометрическому уклону:
,
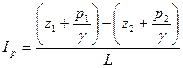а при равномерном безнапорном – геометрическому
.
Движение жидкости может проявляться в двух различных по структуре режимах - ламинарном и турбулентном. Режим движения жидкости зависит от числа Рейнольдса, которое может быть вычислено по диаметру d (для круглых труб)
или через гидравлический радиус R
.
Здесь 
- кинематический коэффициент вязкости м2/c;
m - динамический коэффициент вязкости кгс.с/м2 ;
r - плотность жидкости, кг.с2 /м4 (размерность в системе мкгcс).
По опытным данным Рейнольдса устойчивый ламинарный режим наблюдается (в рассматриваемом им случае напорного движения в трубах), когда число Red < 2300 (ReR < 575). Когда это число больше 2300 (575) - наблюдается турбулентный режим. Для открытых потоков ReRкр =300.
Потери напора по длине потока учитываются седьмым членом уравнения Бернулли – hw, при этом они подразделяются на два вида:
1) потери напора на трение по длине
;
2) потери от местных сопротивлений
,
где l - коэффициент трения;
L - длина прямолинейного участка трубы;
d - внутренний диаметр трубы
- коэффициент сопротивления на трение по длине потока;
zм.с. – коэффициент местного сопротивления;
- скоростной напор в трубе.
Рассмотрим несколько примеров задач гидродинамики.
Пример 1.
Определить расход воды Q в системе, указанной на рисунке. Построить пьезометрическую линию.
Исходные данные:
H = 10 м; l1 = 25 м; d1 = 150 мм; l2 =10 м; d2 =125 мм; l3 =15 м;
d3 =125 мм; a = 45°.
В конце системы имеется вентиль обыкновенный.
Поможем написать любую работу на аналогичную тему