Исчерпание несущей способности длинных гибких стержней, работающих на осевое сжатие, происходит от потери устойчивости (рис.2.4,а).
Поведение стержня под нагрузкой характеризуется графиком (рис.2.4,б), где вначале с ростом нагрузки стержень сохраняет прямолинейную форму, с дальнейшим ростом нагрузки, когда 
стержень теряет свою устойчивость и начинает выпучиваться. Последующий (небольшой) рост внешней нагрузки сопровождается быстрым увеличением поперечного прогиба f. После достижения максимальной нагрузки – второй критической силы 
- стержень теряет несущую способность (неустойчивое состояние).
Устойчивое состояние может быть при 
и 
(точки 1 и 2). Однако при 
стержень может находиться в устойчивом состоянии (точка 2) и
неустойчивом (точка 3) при одинаковой сжимающей силе.
Критическое состояние может быть при 
и при 
(точки 
и 
).
Соответствующее критическое напряжение будет
Ncr1 π2ΕІ π2Εί2 π2Ε
Ơсr =-------- = ----- -- = --------- = ------- (2.16)
A lo2A
lo2 λ2
где 
- критическая сила равная π2ΕI /lo2 (формула Эйлера); 
- площадь поперечного сечения стержня; заменяя I / A получаем i =
- радиус инерции; 
- гибкость стержня; 
- расчетная длина стержня; 
- коэффициент приведения, зависящий от способа закрепления концов стержня.
 |
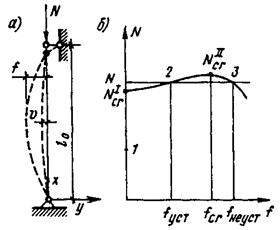Рис.2.4. Работа центрально-сжатого стержня:
а – расчетная схема; б – зависимость между
нагрузкой и прогибом стержня
Формула справедлива при постоянном 
, т.е. при напряжениях 
, при этом 
. Напряжения 
- предел пропорциональности.
На практике гибкость центрально сжатых стержней (колонн, элементов ферм, рам и т.д.) составляет примерно половину указанных предельных.
На рис.2.5 показано влияние сечения стержня на критические напряжения. Из приведенных данных видно, что кривые 
для различных сечений и
Разной ориентации осей будут разными. Кривая для двутавра по рис.2.5,а располагается левее, а по рис.2.5,б – правее кривой, соответствующей прямоугольному сечению (рис.2.5,в).
В приведенной классической схеме, в которой предполагается, что в момент потери устойчивости нагрузка остается постоянной, тогда на выпуклой стороне стержня происходит разгрузка и материал начинает работать по упругому
закону. Однако, если деформация сжатия в процессе продольного изгиба растет
или остается постоянной в каждой точке сечения стержня, т.е. разгрузки не происходит, то все сечение находится в пластическом состоянии, характеризуемом касательным модулем деформации 
.
 |
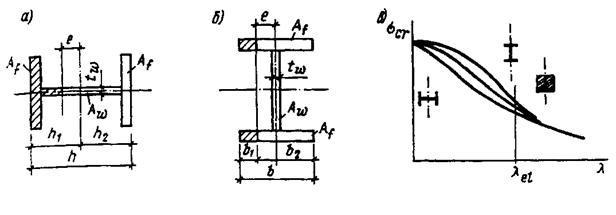Рис.2.5. Влияние формы поперечного сечения стержня на критические напряжения:
а – потеря устойчивости двутаврового стержня в плоскости стенки; б – то же, в
плоскости полок; в – зависимость критических напряжений от гибкости
В этом случае критическое напряжение в пластической области будет
(2.17)
В строительных конструкциях встречаются обе схемы работы сжатых стержней. Например, сжатые элементы статически неопределимых систем (ферм, рам) теряют устойчивость по классической схеме - с разгрузкой. В момент потери устойчивости происходит перераспределение усилий между элементами. В колоннах, работающих по статически определимой схеме, будет реализовываться вторая схема – без разгрузки.
До сих пор рассматривался идеально прямой стержень с нагрузкой, приложенной строго по оси. Однако в практике такого не существует. Конструктивное оформление концов сжатых стержней не обеспечивает идеальную центровку, поэтому эти факторы учитываются введением в расчет эквивалентного эксцентриситета сжимающей силы “
”. Он зависит от гибкости и с ростом ее возрастает. В практических расчетах пользуются 
, т.е. со случайным эксцентриситетом. Тогда
, (2.18)
где 
- коэффициент устойчивости или его еще называют коэффициентом предельного изгиба при центральном сжатии.
В нормах на проектирование даются формулы и соответствующие таблицы для определения 
.
Поможем написать любую работу на аналогичную тему