Потеря несущей способности длинных гибких стержней при одновременном действии сжимающей силы и изгибающего момента происходит от потери устойчивости. При этом соответствующее состояние равновесия можно определить так же, как для центрального сжатия, а именно 
- устойчивое состояние; 
- неустойчивое состояние; 
- критическое состояние (где 
и 
- приращение работ внешних и внутренних сил).
Внецентренно сжатые стержни реальных металлических конструкций теряют устойчивость при развитии пластических деформаций.
Критическая сила зависит от эксцентриситета “e”. На практике удобнее пользоваться безразмерным относительным эксцентриситетом m=e/ρ, где ρ=W/A - ядровое расстояние со стороны наиболее сжатой фибры стержня.
Формула проверки устойчивости внецентренно сжатого стержня будет
N / (Aφe ) 
Ry γc (2.19)
Для обеспечения устойчивости внецентренно сжатых (сжато-изогнутых) стержней целесообразно с целью экономии металла развивать сечение в направлении эксцентриситета. Например, как показано на рис.2.6. При этом возрастает опасность потери устойчивости стержня в перпендикулярном направлении – относительно оси “y” . В связи с этим в формулу проверки устойчивости относительно оси “y” вводится пониженный коэффициент с.
N / cφyA 
γcRy (2.20)
где с =Ncr.M/Ncr =φy.M/φy; φy.Ncr –соответственно коэффициент устойчивости и критическая сила при центральном сжатии; Ncr.M. φy.M – критическая сила и соответствующий коэффициент устойчивости центрального сжатия относительно оси “y” при наличии момента в перпендикулярной плоскости. Коэффициент “c” зависит от относительного эксцентриситета mx=e/ρx.формы поперечного сечения стержня и гибкости λy.
 |
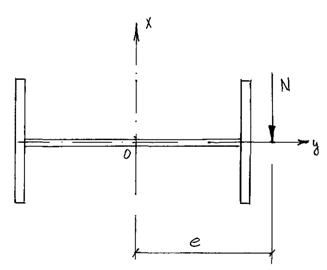Рис.2.6. Наиболее рациональное положение двутаврового сечения при внецентренном сжатии стержней
|
Поможем написать любую работу на аналогичную тему
Получить выполненную работу или консультацию специалиста по вашему
учебному проекту
Узнать стоимость |