Расчет изгибаемых элементов в упругой стадии и с учетом развития пластических деформаций

Расчет конструкции обычно состоит из следующих этапов: установление расчетной схемы, сбор нагрузок, определение усилий в элементах конструкции, подбор сечений и проверка напряженно-деформированного состояния конструкции в целом, ее элементов и соединений с целью не допустить ни одного из предельных состояний.

Согласно Своду правил элементы конструкций подразделяются на три класса в зависимости от напряженно-деформированного состояния расчетного сечения (табл. 3.1):

Таблица 3.1

Классы напряженных состояний сечений при изгибе

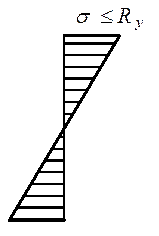
1-й класс – напряженно-деформированное состояние, при котором напряжения в сечении не превышают расчетное сопротивление стали σ ≤ Ry (упругая работа сечения);

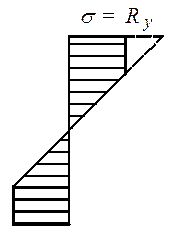
2-й класс – напряженно-деформированное состояние, при котором в одной части сечения σ < Ry, а в другой σ = Ry  (упруго-пластическая работа сечения);

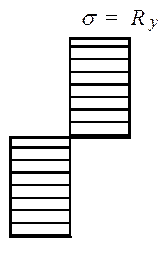
3-й класс – напряженно-деформированное состояние, при котором по всей площади сечения σ = Ry (пластификация всего сечения, условный пластический шарнир).

Класс напряженного состояния сечения при проектировании следует назначать в зависимости от допустимых пластических деформаций, целесообразных размеров сечения элемента в целом, толщины стенок и поясных листов. Следует учитывать назначение конструкции, характер нагрузок и воздействий, опасность хрупкого разрушения, агрессивность среды, конструктивные ограничения, степень огнестойкости и другие факторы.

Расчет на прочность балок в упругой стадии работы сечения выполняют по формулам:

– при действии момента в одной из главных плоскостей

,

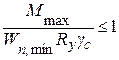где    Mmax – максимальныq изгибающий момент от расчетной нагрузки;

Wn,min – момент сопротивления ослабленного сечения;

– при действии в сечении поперечной силы

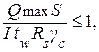
где    Q – максимальная поперечная сила от расчетной нагрузки;

I – момент инерции сечения;

S – статический момент сдвигаемой части сечения относительно нейтральной оси;

tw – толщина стенки.

При изгибе в двух главных плоскостях проверку сечения проводят по формуле

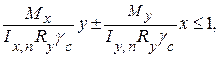
где    Mx и My  –моменты относительно осей соотвественно x-x и y-y;

Ix,n и Iy,n – моменты инерции относительно главных осей ослабленного сечения;

x и y – координаты рассматриваемой точки сечения относительно главных осей.

Расчет на прочность разрезных балок в упругопластической стадии работы двутаврового сечения из стали с нормативным сопротивлением            Ry ≤ 440 МПа, несущих статическую нагрузку, при передаче нагрузки через сплошной жесткий настил, непрерывно опирающийся на сжатый пояс балки и надежно с ним связанный (плоский металлический настил, железобетонные плиты и т.п.), и при ограничении касательных напряжений в месте максимального момента t = Q/Aw £ 0,9Rs (кроме опорных сечений) при изгибе в плоскости наибольшей жесткости (Ix > Iy) относительно оси x-x выполняют с учетом развития пластических деформаций в узкой локализованной зоне по формуле

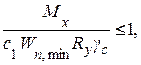
где   Mx – максимальный изгибающий момент, действующий в плоскости наибольшей жесткости;

c1 – коэффициент, учитывающий резерв несущей способности изгибаемого элемента, обусловленный пластической работой материала. Он зависит от формы сечения, отношения площадей поперечного сечения пояса и стенки αf  = Af /Aw, принимается: c1 = c при t £ 0,5Rs (влияние касательных напряжений на переход в предельное состояние считается несущественным), где с определяется по табл. 3.2;  c1= 1,05βс = 1,05с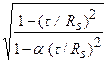 при

0,5Rs < t £ 0,9Rs, (зависит от значения средних касательных напряжений в сечении t = Q/(twhw), здесь α – коэффициент, равный 0,7 для двутаврового сечения, изгибаемого в плоскости стенки; α = 0 для других типов сечений; tw и hw  – толщина и высота стенки.

Таблица 3.2

Значения коэффициентов с, (cx), cy

При наличии ослаблений стенки отверстиями для болтов значения касательных напряжений t  определяются с учетом ослаблений (следует умножитьt на коэффициент ослабления α = а/(а – d), где а – шаг отверстий; d – диаметр отверстия).

Для элементов, изгибаемых в двух главных плоскостях, проверка прочности сечения ведется по формуле

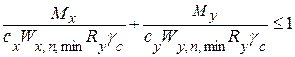
при ограничении касательных напряжений условием t £ 0,5Rs. Значения коэффициентов cx и cy, учитывающих развитие пластических деформаций, принимается из табл. 3.2.

При расчете сечения в зоне чистого изгиба, где зона пластических деформаций большой протяженности, вместо коэффициента c1 принимают

с1m = 0,5(1 + c1).

Для балок, рассчитываемых с учетом пластических деформаций, расчет на прочность в опорном сечении (при Mx = 0) выполняют по формуле

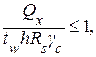
где    Qx – максимальная поперечная сила на опоре;

h – высота сечения балки.

При ослаблении стенки отверстиями для болтов левую часть формулы умножают на коэффициент ослабления α.

Расчет на прочность балок переменного сечения с учетом развития пластических деформаций следует выполнять только для одного сечения с наиболее неблагоприятным сочетанием усилий M и Q; в остальных сечениях учитывать развитие пластических деформаций не допускается.