Расчет прокатной балки, работающей на косой изгиб

На косой изгиб рассчитываются конструкции, изгибаемые в двух плоскостях. К таким конструкциям обычно относятся прогоны кровли с уклоном при опирании их на стропильные фермы.

Уклон кровли относительно невелик и скатная составляющая нагрузки qy в 3 – 6 раз меньше qx, однако жесткость прогона в плоскости ската мала (соотношение Wy/Wx составляет 1/6 – 1/8), следовательно, напряжения от скатной составляющей получаются большие, а суммируясь с напряжением от qx могут превысить расчетное сопротивление стали.

Общая устойчивость прогонов обеспечивается элементами крепления кровельных плит или настила к прогонам и силами трения между ними. Однако на практике силы трения при свободном опирании кровельных элементов могут оказаться недостаточными, тогда возможна потеря устойчивости прогона.

Пример 3.3. Подобрать сечение прогона из прокатного швеллера пролетом l = 6 м, шаг прогонов b = 3 м. Уклон кровли i = 1:6 (угол α = 9,5º). Расчетная нагрузка g = 1,43 кН/м2, нормативная – gn = 1,17 кНм2.

Прогон с сечением из швеллера следует устанавливать стенкой по направлению ската (рис. 3.6), чтобы уравновесить крутящий момент от составляющей qy, приложенной на верхнем поясе.

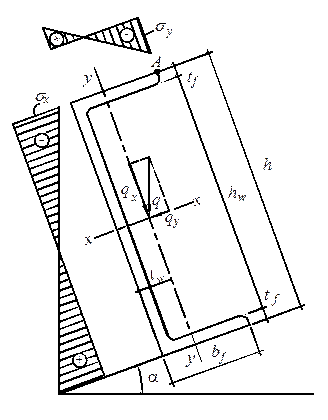
Рис. 3.6. К расчету прогона

Определяем вертикальные погонные нагрузки на прогон:

– нормативную

qn = gnb = 1,17 × 3 = 3,51 кН/м;

– расчетную

q = qb = 1,43 × 3 = 4,29 кН/м.

Раскладываем вертикальную расчетную нагрузку на составляющие, действующие в двух плоскостях изгиба:

qx = q сosα = 4,29 × 0,986 = 4,23 кН/м;

qy = q sinα = 1,29 × 0,165 = 0,71 кН/м.

где     сosα = сos 9,5º = 0,986; sin 9,5º = 0,165.

Расчетные изгибающие моменты:

Mx = qxl2/8 = 4,23 × 62 / 8 = 19,04 кН·м;

My = qyl2/8 = 0,71 × 62 / 8 = 3,2 кН·м.

Подбор сечения прогона выполняем по упругой стадии работы материала.

Несущую способность прогона при изгибе в двух плоскостях проверяем по прочности (наиболее напряженная точка А).

Нормальное напряжение

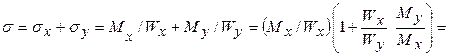
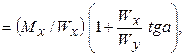
где     My/Mx = tga = tg 9,5о = 0,167;

Wx/Wy ≈ 6 – 8 – отношение моментов сопротивления сечения для прокатных швеллеров (предварительно принимаем Wx/Wy  = 7).

Условие прочности

s = (Mx/Wx) (1 + 7tgα) £ Rygc,

откуда определяем требуемый момент сопротивления:

Wx,min = Mx(1 + 7 × 0,167)/(Rygc) = 1904 × 2,17 / (24 × 1) = 172,15 см3.

Принимаем сечение прогона по сортаменту ГОСТ 8240-93 из . Значение jb определяют с учетом влияния возможного развития пластических деформаций при совместном действии косого изгиба и кручения в момент потери устойчивости.

Для определения коэффициента jb предварительно вычисляем коэффициент j1. Для балок двутаврового сечения с двумя осями симметрии он определяется по формуле

,

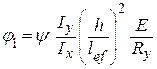где значение y следует принимать по табл. 3.6 в зависимости от характера нагрузки и параметра α;

h = 22 см – полная высота сечения;

lef – расчетная длина балки, равная расстоянию между точками закреплений сжатого пояса от поперечных смещений (в примере lef = l = 6 м – при отсутствии связей).

Для балок швеллерного сечения коэффициент jb следует определять как для балок симметричного двутаврового сечения, при этом значения α необходимо вычислять по формуле

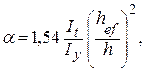
здесь It – момент инерции сечения при кручении.

Вычисленные значения j1 необходимо умножить на 0,7. Значения Ix, Iy, и It в формулах следует принимать для швеллера.

Определяем параметр α:

 1,54 (6,43 / 154) (600 / 22)2 = 47,83,

где    It для швеллера определяют по формуле

It = (1,12 / 3) (2bf tf3 + hwtw) = (1,12 /3) (2 × 8,2 × 0,953 + 20,1 × 0,543) = 6,43см4.

Для балки без закреплений и равномерно распределенной нагрузки по верхнему поясу при α = 47,83

y = 3,15 + 0,04α – 2,7 × 10–5α2 = 3,15 + 0,04 × 47,83 – 2,7 × 10–5 × 47,832 = 5,0.

Таблица 3.6

Коэффициенты y для двутавровых балок

с двумя осями симметрии

П р и м е ч а н и е. Значение Y1 следует принимать равным Y при двух и более закреплениях сжатого пояса в пролете.

Определяем коэффициент j1:

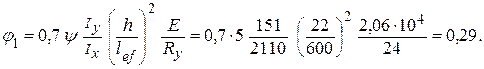
Значение коэффициента jb необходимо принимать:

– при j1 £ 0,85   jb = j1;

– при j1 > 0,85   jb = 0,68 + 0,21 j1, но не более 1,0.

Принимаем jb = j1 = 0,290.

Проверяем устойчивость прогона:

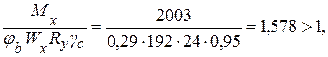
Общая устойчивость прогона не обеспечена. Значит необходимо увеличить сечение до нужных размеров, обеспечивающих выполнение условия устойчивости прогона, приняв больший номер швеллера. Проверка показала, что прогон из :

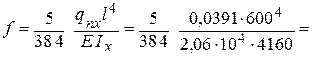0,77 см < fu = 3 см,

где     qnx = qn cosa = 3,97 × 0,986 = 3,91 кН/м = 0,0391 кН/см;

fu = l/200 = 600 / 200 = 3 см – предельный прогиб прогона открытого для обозревания при пролете l = 6 м (см. табл. 1.4).

Жесткость прогона обеспечена.