Подбор сечений элементов фермы - МЕТАЛЛИЧЕСКИЕ КОНСТРУКЦИИ. Курс лекций

При подборе сечений элементов ферм для удобства комплектования металла, необходимо стремиться к возможно меньшему числу различных номеров и калибров уголковых профилей, ограничиваясь обычно 6 – 8.

При значительных усилиях в элементах ферм возможно применение двух классов стали: более высокой прочности – для сильно нагруженных поясов и опорных раскосов; малоуглеродистой стали обыкновенного качества – для элементов решетки.

Подбор сечения начинается с подбора сечения сжатого элемента, имеющего наибольшее расчетное усилие. При выборе уголковых профилей для сжатых элементов следует стремиться к применению уголков возможно меньшей толщины, поскольку их радиусы инерции имеют относительно большие значения. Во избежание повреждения ферм во время перевозки и при монтаже принимается минимальный уголок ∟50×50×5.

Для снижения трудоемкости изготовления в фермах пролетом до 24 м включительно, состоящих из двух отправочных марок, пояса принимаются постоянного сечения, подобранного по максимальному усилию. В стропильных фермах пролетом 30 м и более сечение поясов по длине рационально изменять, при этом лучше изменять только ширину полок, сохраняя неизменной толщину уголков, чтобы облегчить устройство стыков.

Подбор сечений сжатых элементов ферм производится, как правило, из условия устойчивости элемента, растянутых – из условия прочности. Длинные слабо нагруженные элементы подбираются по предельной гибкости. При расчетах на устойчивость сжатых элементов стержневых конструкций покрытий и перекрытий (за исключением замкнутых трубчатых сечений) вводится коэффициент условий работы γс = 0,95; при расчете сжатых элементов (кроме опорных) решетки составного таврового сечения из уголков сварных ферм покрытий и перекрытий (например, стропильных и аналогичных им ферм) при гибкости λ ≥ 60 вводится коэффициент условий работы γс = 0,8.

При расчете соединений (кроме стыковых соединений) рассматриваемых выше элементов коэффициенты условий работы γс = 0,95 и γс  = 0,8 учитывать не следует.

Подбор сечений элементов ферм оформляется в табличной форме.

Для примеров геометрическая схема фермы с расчетными усилиями в стержнях представлена на рис. 5.1.

Пример 5.1. Подобрать сечение верхнего сжатого пояса фермы из двух уголков при действии на него расчетного усилия N = – 1300 кН. Расчетные длины стержней: в плоскости фермы 3 м, из плоскости – 3 м (при шаге прогонов  кровли d = 3 м). Материал – сталь класса С245 (район ІІ4, здание отапливаемое); Ry = 24 кН/см2; γс = 0,95 (см. табл. 1.3). Максимальное усилие в опорном раскосе Np,max = – 670 кН.

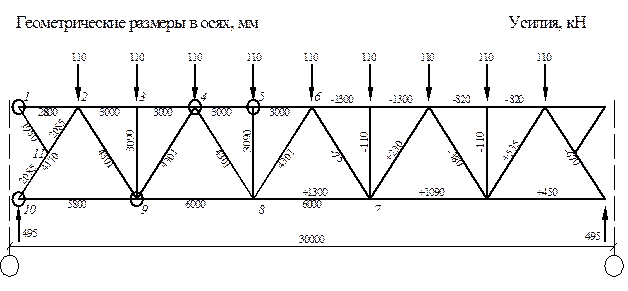
Рис. 5.1. Расчетная и геометрическая схемы фермы

Толщину фасонок выбирают в зависимости от действующих усилий в элементах решетки (табл. 5.6). Принимаем толщину фасовки tф = 14 мм при максимальном усилии в олорном раскосе 670 кН.

Таблица 5.6

Рекомендуемые толщины фасонок

Поскольку ly  = lx, принимаем сечение  сжатого пояса из двух равнополочных уголков (рис. 5.2).

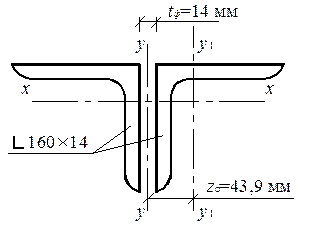
Рис. 5.2. Сечение пояса (к примеру 5.1)

При предварительном подборе сечения поясов легких ферм гибкость принимается λ = 60 – 90. Большие значения гибкости принимаются при меньших усилиях.

Задаемся λ = 70. Условная гибкость

По условной гибкости для для типа кривой устойчивости ′′с′′ (см.   табл. 3.12) определяем коэффициент устойчивости j  = 0,674 (см. табл. 3.11).

Из условия устойчивости сжатого стержня определяем требуемую площадь сечения пояса:

Атр = N/(φRyγс) = 1300 / (0,674 ∙ 24 ∙ 0,95) = 84,6 см2.

Требуемый радиус инерции

iтр = lx/λ = 300 / 70 = 4,29 см.

По требуемым значениям площади и радиуса инерции из сортамента

принимаем сечение из двух равнополочных уголков∟160×160×14/ГОСТ 8509-93. Площадь сечения А = 43,57 ∙ 2 = 87,14 см2; радиус инерции относительно оси х-х – iх = 4,92 см; радиус инерции одного уголка относительно собственной центральной оси, параллельной свободной, iy = 4,92 см; расстояние от центра тяжести уголка до наружной грани полки, параллельной оси y1-y1,  zо = 4,47 см.

Определяем радиус инерции составного сечения из двух уголков при зазоре между уголками (толщина фасонки) а =  tф = 14 мм:

см.

Подсчитываем гибкости в главных плоскостях:

λх = lx/iх = 300 / 4,92 = 61;

λу = lу/iу = 300 / 7,14 = 42.

Наибольшая условная гибкость

По табл. 3.11. находим минимальный коэффициент φmin = 0,730.

Производим проверку устойчивости центрально-сжатого пояса:

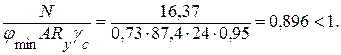
Недонапряжение

Максимальная гибкость

λх = 60,7 < λи = (180 – 60α) = (180 – 60 · 0,896) = 126,

где    α = 0,896 – степень загруженности стержня.

В процессе монтажа (раскрепляющие верхний сжатый пояс прогоны или плиты покрытия отсутствуют) в предположении строповки фермы в узлах верхнего пояса через четыре панели гибкость пояса из плоскости фермы не должна превышать предельной

λу  = lу / iу  = 4 d / i y  = 4 ∙ 300 / 7,1 = 169 < λи = 220.

Сечение из двух уголков ∟160×160×14 принято.

Пример 5.2. Подобрать сечение верхнего сжато-изгибаемого пояса при действии  на  него  осевого  усилия   N = – 1300 кН  и  внеузловой  нагрузки  F = 55 кН, приложенной в середине панели d (расчетная схема представлена на рис. 5.3). Расчетная длина пояса λх = λу = d = 3 м.

Материал конструкции – сталь класса С245. Расчетное сопротивление Ry = 24 кН/см2. Коэффициент условий работы γс = 0,95.

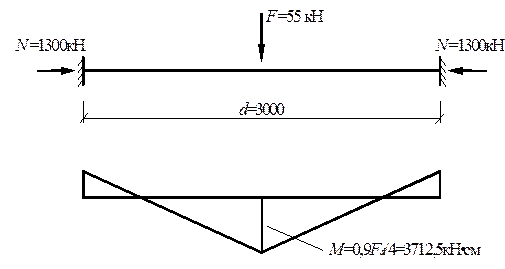
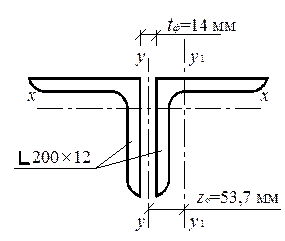
Рис. 5.3. Расчетная схема и сечение пояса

Определяем изгибающий момент в середине панели пояса

M = 0,9Fd/4 = 0,9 ∙ 55 ∙ 300 / 4 = 3712, 5 кН∙см.

Эксцентриситет

е = M/N = 3712,15 / 1300 = 2,86 см.

Расчет на устойчивость внецентренно-сжатых и сжато-изгибаемых элементов выполняется как в плоскости действия момента (плоская форма потери устойчивости), так и из плоскости действия момента (изгибно-крутильная форма потери устойчивости).

Расчет таких элементов постоянного сечения в плоскости действия момента, совпадающей с плоскостью симметрии, производится по формуле

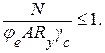
Таблица 5.7

Коэффициент влияния формы сечения η

В формуле φе  – коэффициент устойчивости при сжатии с изгибом определяется для сплошностенчатых стержней в зависимости от условной гибкости  и приведенного относительного эксцентриситета mef (табл. 8.2), определяемого по формуле mef  = ηm,

где   η – коэффициент влияния формы сечения, определяемый по табл. 5.7 (предварительно для таврового сечения принимается η = 1,8);

m = e/ρx = eA/Wc – относительный эксцентриситет;

ρx = Wc/A – ядровое расстояние; Wc = Ix /z0 – момент сопротивления сечения для наиболее сжатого волокна; z0 ≈ 0,3h –расстояние от центра тяжести до наиболее сжатого волокна для таврового сечения; h – высота сечения.

При предварительном подборе сечения для поясов принимается гибкость λ = 60 – 90.

Задаемся гибкостью λх = lx /iх = 60.

Определяем отвечающие этой гибкости и расчетной длине стержня lx:

– радиус инерции

ix,тр = lx /λx = 300 / 60 = 5 см;

– требуемую высоту сечения

h = ix/α1 = 5 / 0,3 ≈ 17 см (принимаем h = 18 см),

где    α1 ≈ 0,3 для таврового сечения из двух равнополочных уголков;

– ядровое расстояние

rx = Wc /A = (Ix /A)/z0 = i2x /z0 = (0,3h)2 / (0,3h) = 0,3h = 0,3 ∙ 18 = 5,4 см;

– приведенный эксцентриситет

mef  = ηe/ρx = 1,8 ∙ 2,86 / 5,4 = 0,95;

– условную гибкость

.

По условной гибкости  и приведенному эксцентриситету mef  принимаем φе = 0,543.

Требуемая площадь сечения пояса

Aтр = N/(φеRyγc) = 1300 / (0,543 ∙ 24 ∙ 0,95) = 105 см2.

По Aтр и iх,тр по сортаменту принимаем сечение из двух равнополочных уголков ∟200×200×12 / ГОСТ 8510-86, имеющих характеристики:

А = 2 ∙ 47,1 = 94,2 см2; Ix = 2 ∙ 1822,78 = 3645,36 см4; iх = 6,22 см;  zо = 5,37 см.

Определяем:

– момент сопротивления сечения для наиболее сжатого волокна

Wc = Ix /zо = 3645,56 / 5,37 = 678,88 см3;

– ядровое расстояние

ρx = Wc/А = 678,88 / 94,2 = 7,2 см;

– относительный эксцентриситет

m = e/ρx = 2,86 / 7,2 = 0,4;

– гибкость

λх = lx /iх = 300 / 6,22 = 48,2;

– условную гибкость

– по табл. 5.7 при Af /Aw  = 1 и  = 1,64 вычисляем

η = 1,8 + 0,12m = 1,8 + 0,12 ∙ 0,4 = 1,85;

– приведенный эксцентриситет

mef  = ηm = 1,85 ∙ 0,4 = 0,74.

По  = 1,64 и mef  = 0,74 определяем φе = 0,640.

Производим проверку пояса в плоскости действия момента:

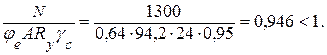
Недонапряжение

Проверяем устойчивость пояса фермы из плоскости действия момента, для чего определяем:

– радиус инерции таврового сечения

см;

– момент инерции

Iy = iy2A = 8,72 ∙ 94,2 = 7130 см4;

– гибкость

λу = lу/iу = 300 / 8,7 = 34,5.

Так как гибкость стержня λу = 34,5 < λх = 48,2 (жесткость ЕIy > EIx), проверка устойчивости пояса из плоскости действия момента не требуется.

При ЕIy < ЕIx проверка устойчивости сжато-изогнутого пояса из плоскости действия момента производится по формуле

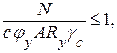
где    φy – коэффициент устойчивости при центральном сжатии относительно оси y-y, принимается по условной гибкости  (см. табл. 3.11);

с – коэффициент, учитывающий изгибно-крутильную форму потери ус-

тойчивости и зависящий от относительного эксцентриситета и формы сечения, принимается по .

При подборе сечения внецентренно-сжатых или сжато-изгибаемых элементов можно было воспользоваться наиболее простым, но менее точным способом определения требуемой площади сечения – методом последовательных приближений. Поскольку осевое усилие N играет определяющую роль, предварительно (с некоторым запасом) принимается сечение из расчета на усилие N как центрально-сжатого элемента, а затем оно проверяется с учетом действующего момента как внецентренно-сжатый элемент.

Пример 5.3. Подобрать сечение стержней растянутого нижнего пояса стропильной фермы по максимальному расчетному усилию в середине пролета Nmax = 1300 кН и минимальному расчетному усилению в крайней панели

Nmin = 450 кН. Расчетная длина стержня в плоскости фермы lx = 6 м. Материал конструкции – сталь С245; Ry = 24 кН/см2 – расчетное сопротивление стали, коэффициент условий работы γс = 0,95.

Несущую способность элементов, выполненных из стали с нормативным сопротивлением Ryn ≤ 440 МПа и имеющих развитую площадку текучести, проверяют, исходя из условия развития пластических деформаций, по формуле

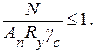
Для элементов, выполненных из сталей, не имеющих площадки текучести (условный предел текучести σ02 > 440 МПа), а также,  если эксплуатация конструкций возможна и после развития пластической деформации, проверка несущей способности производится по формуле

где    Ru – расчетное сопротивление стали, определенное по временному сопротивлению (см. табл. 2.3); γu = 1,3 – коэффициент надежности при расчете по временному сопротивлению; Aп – площадь сечения нетто с учетом возможных ослаблений отверстиями под болты или заклепки; для сварных конструкций Aп = Авr.

Определяем требуемую площадь сечения нижнего пояса по максимальному усилию:

Aтр = Nmax /(Ryγc) = 1300 / (24 ∙ 0,95) = 57,02 см2.

Принимаем сечение из двух неравнополочных уголков, составленных узкими полками, ∟160×100×12, имеющих площадь сечения  А = 30,04 ∙ 2 =

= 60,08 см2 > Aтр = 57,02 см2; радиус инерции стержня в плоскости фермы          ix = 2,18 см; zо= 2,36 см.

Проверяем растянутый пояса на прочность:

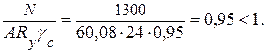
Проверяем гибкость в вертикальной плоскости (см. табл. 5.3):

λх = lx/iх = 600 / 2,18 = 275 < λи = 400.

Определяем площадь сечения по минимальному усилию

Aтр = Nmin/(Ryγc) = 450 / (24 ∙ 0,95) = 19,74 см2.

Принимаем сечение их двух неравнополочных уголков ∟100×63×7, составленных узкими полками,  имеющих площадь  сечения  А = 11,09 ∙ 2 =

= 22,18 см2 > Aтр = 19,74 см2; радиус инерции ix = 1,37 см; zо = 1,46 см.

Проверяем гибкость в вертикальной плоскости:

λх = lx/iх = 600 / 1,37 = 438 > λи = 400.

Нижний пояс по гибкости не проходит. Принимаем сечение их двух равнополочных уголков ∟90×90×7, имеющих площадь сечения

А = 12,28 ∙ 2 = 24,56 см2 > Aтр = 19,74 см2; радиус инерции ix = 2,77 см;              zо = 2,47 см.

Гибкость в вертикальной плоскости

λх = lx/iх = 600 / 2,77 = 217 < λи = 400.

Проверяем пояса на прочность:

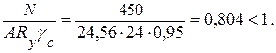
Сечение удовлетворяет условиям прочности и предельной гибкости.

Пример 5.4. Подобрать сечение сжатого среднего раскоса фермы по расчетному усилию N = – 75 кН. Расчетные длины раскоса: из плоскости фермы ly = l = 4300 мм; в плоскости фермы lx = 0,8l = 0,8 ∙ 4300 = 3440 мм. Материал конструкций – сталь С245.

Сечение средних малонагруженных элементов решетки фермы, как правило, подбирается по предельной гибкости λи.

В соответствии с табл. 5.2 для сжатого раскоса λи = 210 – 60a.

Предварительно принимаем коэффициент a = 0,75, тогда

λи = 210 – 60 ∙ 0,75 = 165.

Требуемые радиусы инерции:

– при расчете в плоскости фермы

ix,тр = lx/λи = 344 / 165 = 2,08 см;

– при расчете из плоскости фермы

iу,тр = lу /λи = 430 / 165 = 2,61 см.

По сортаменту принимаем сечение раскоса из двух равнополочных уголков ∟70×70×5, для которых ix = 2,16 см > ix,тр = 2,08 см;

 см > iу,тр,

где    zо= 1,9 см; a = tф = 14 мм; площадь сечения А = 2 ∙ 6,86 = 13,72 см2.

Гибкости раскоса:

λx  = lx/ix = 344 / 2,16 = 159 < λи = 165;

λу  = lу/iу = 430 / 3,38 = 127 < λи.

Максимальная условная гибкость раскоса

при которой коэффициент устойчивости φ = 0,253,

Проверяем устойчивость раскоса:

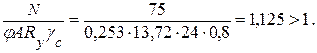
где    γc = 0,8 при λ ≥ 60 (см. табл. 1.3).

Сечение их двух уголков ∟70×70×5 подобрано неудачно и не удовлетворяет условию устойчивости. Принимаем сечение из двух уголков ∟75×75×5, для которых: А = 2 ∙ 7,39 = 14,78 см2; ix = 2,31 см; zо = 2,02 см; см.

Подсчитываем гибкости:

λх = lx/ix = 344 / 2,31 = 149;

λу = lу /iу = 430 / 3,57 = 120.

Наибольшая условная гибкость

Коэффициент устойчивости φ = 0,282.

Производим проверку раскоса на устойчивость:

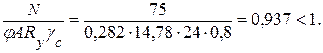
Степень загруженности элемента α = 0,937.

Предельная гибкость

λи = 210 – 60α = 210 – 60 ∙ 0,937 = 154.

Проверяем гибкость стержня

λх = 149 < λи = 154.

Сечение из двух уголков ∟75×75×5 удовлетворяет условиям устойчивости и предельной гибкости.

Подбор сечений остальных элементов фермы произведен в табличной форме (табл. 5.8). Окончательно сечения элементов фермы приняты с учетом унификации калибров уголков.