Проверка устойчивости подкрановой части колонны

Уточняем положение центра тяжести принятого сечения колонны:

hо = hн –  zо.= 1250 – 150 = 1100 мм;

y1 = Aв2hо /(Aв1 + Aв2) = 145,7 × 110 / (102,8 + 145,7) = 64,5 см;

y2= hо – y1 = 110 – 64,5 = 45,5 cм.

Вычисляем фактические расчетные усилия в ветвях:

Nв1 = N1y2/hо + M1/hо = 2468,1 × 0,455 / 1,1 + 1112,7 / 1,1 = 2032,44 кН;

Nв2 =N2y1/hо + M2/hо = 2473,5 × 0,645 / 1,1 + 1589,4 / 1,1 = 2895,28 кН.

Проверяем устойчивость ветвей колонны из плоскости действия момента:

– подкрановой ветви

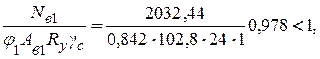
где    j1 = 0,842 – коэффициент устойчивости, принимаемый по табл. 3.11 для кривой устойчивости ′′b′′ в зависимости от условной гибкости

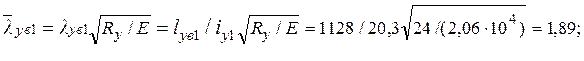
– наружной ветви

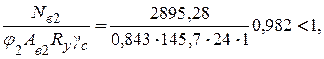
где   j2 = 0,843 – коэффициент устойчивости, принимаемый в зависимости от условной гибкости

Ветви колонны из плоскости действия момента устойчивы.

Проверка устойчивости ветвей колонны в плоскости действия момента (относительно осей х1-х1 и х2- х2).

Определяем гибкости ветвей:

– подкрановой относительно оси х1-х1

lxв1 = lхв1/iх1 = 220 / 4,27 = 51,52 < lyв1 = 55,57;

– наружной относительно оси х2-х2

lxв2 = lхв2 /iх2  = 220 / 6,81 = 32,31 < l yв2 = 55,16,

где    lхв1 = lхв2 – расчетные длины ветвей в плоскости действия момента, равные величине панели решетки lв (рис. 8.5).

Величина панели lв назначается исходя из условий равноустойчивости ветвей в двух плоскостях (lxв1 = lув1  и l xв2 = l ув2).

Рис. 8.5. К определению величины панели решетки

Принимается  lв минимальная из двух значений:

lхв1 = lyв1 iх1 = 55,57 × 4,27 = 237,3 см;

lхв2 = lyв2 iх2 = 55,16 × 6,81 = 375,6 см;

tga = 2hо /lв = 2 × 110 / 237,3 = 0,93.

Угол наклона раскоса к ветви a  = 42,9°.

Рекомендуется из конструктивных соображений 45° £ a £ 55°.

Принимаем a = 45°; lв  = 220 см.

При lxв1 = lув1  и lxв2 = lув2  проверку устойчивости ветвей в плоскости действия момента можно не производить.

Для проверки устойчивости колонны как единого стержня составного сечения относительно оси х-х необходимо найти приведенную гибкость стержня lef, зависящую от площади сечения раскосов.

Раскосы решетки выполняются из горячекатанных уголков (в отдельных случаях из швеллеров малого калибра) и рассчитываются на большую (Qmax) из поперечных сил: фактическую Q, действующую в сечении колонны, или условную Qfic, определяемую по СНиП .

Предварительно сечение раскоса подбираем по фактической силе           Q = 182,6 кН, действующей в нижней части колонны.

Продольное усилие в раскосе одной плоскости решетки

Nd = Q/(2sina) = 182,6 / (2 × 0,707) = 129,14 кН.

Требуемая площадь сечения раскоса

Ad = Nd/(jRygc) = 129,14 / (0,6 × 24 × 0,75) = 11,96 см2,

где    j  принимается ориентировочно в пределах 0,6 – 0,8; gc = 0,75 – коэффициент условий работы, принимаемый по табл. 1.3 для сжатых элементов из одиночных уголков, прикрепленных одной полкой.

По сортаменту принимаем раскос из уголка ∟90×90×7/ГОСТ 8509-03 для которого Ad = 12,28 см2; iyо  = 1,78 см (минимальный относительно       оси yо-yо); расчетная длина ld = hо/sina = 110 / 0,707 = 155,6 см; гибкости:

lmax = ld/iyо = 155,6 / 1,78 = 87,42;

Производим проверку сжатого раскоса на устойчивость по формуле

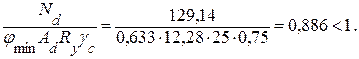
где    jmin = 0,633 – коэффициент устойчивости для типа кривой устойчивости ″b″, принятый по табл. 3.11;

Устойчивость  раскоса обеспечена.

Горизонтальная дополнительная распорка в решетке колонны, поставленная при необходимости для уменьшения расчетной длины ветви колонны, рассчитывается на Qfic или подбирается по предельной гибкости

iтр = lplu,

где    lu = 150.

Определяем геометрические характеристики сквозного сечения колонны:

– площадь А = Ав1 + Ав2 = 102,8 + 176,6 = 279,4 см2;

– момент инерции Ix = Ix1 + Aв1y12 + Ix2+ Aв2y22 =

= 1873 + 102,8 · 64,52 + 6762 + 145,7 · 45,52 = 737944,13 см4;

– радиус инерции

– гибкость стержня колонны относительно свободной оси х-х

lх = lх1/iх = 2820 / 51,39 = 54,87;

– приведенная гибкость

где    a1 – коэффициент, зависящий от угла наклона раскоса к ветви a

(рис. 8.5) и определяемый по формуле

Ad1 = 2Ad = 2 × 12,28 = 24,56 см2 – площадь сечения раскосов решеток, лежащих в плоскостях, перпендикулярных оси х1-х1 (площадь двух раскосов);

– условная приведенная гибкость

Проверка устойчивости подкрановой части колонны производится на обе комбинации расчетных усилий:

– догружающую подкрановую ветвь

N1 = – 2468,1 кН и M1 = – 1112,7 кН×м;

– догружающую наружную ветвь

N2 = – 2473,5 кН и M2  = – 1589,4 кН×м.

Определяем относительный эксцентриситет m1 для комбинации усилий, догружающих подкрановую ветвь:

m1 = (M1 /N1)/r = (111270 / 2468,1) / 40,5 = 1,11,

где    r = Ix/(y1A) = 737944,13 / (64,5 × 279,4) = 40,95 см – радиус ядра сечения.

Находим коэффициент устойчивости при сжатии с изгибом для проверки устойчивости сквозного внецентренно-сжатого стержня с решеткой по табл. 8.3 в зависимости от  и m1 = 1,11 ® je1 = 0,403.

Проверяем устойчивость колонны относительно оси х-х:

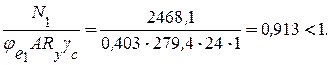
Определяем m2 для комбинации усилий, догружающих наружную ветвь:

m2 = (M2 /N2)/r = (158940 / 2473,5) / 58,05 = 1,11,

где    r = Ix/(y2A) = 737944,13 / (45,5 × 279,4) = 58,05 см.

По табл. 8.3 принимаем je2 = 0,403.

Производим проверку колонны:

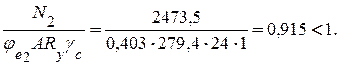
Вычисляем условную поперечную силу по формуле

Qfic = 7,15 × 10–6(2330 – E/Ry)N/j =

= 7,15 × 10–6 (2330 – 2,06 × 104 / 24) × 2473,5 / 0,830 = 31,36 кН < Q  = 182,6 кН,

где    j = 0,830 – коэффициент устойчивости при сжатии, принимаемый для составного стержня в плоскости соединительной решетки по табл. 3.11 в зависимости от

При Qfic £ Q перерасчета сечения раскосов на Qfic и повторной проверки сечения колонны как единого стержня не требуется.

Устойчивость колонны в плоскости действия момента обеспечена.

Устойчивость сквозной колонны  как единого стержня из плоскости действия момента проверять не следует, так как она обеспечена проверкой устойчивости отдельных ветвей.

Проверяем соотношение моментов инерции (жесткостей) нижней и верхней частей колонны: Iн/Iв = 737944,13 / 174581,2 = 4,23. Отличие принятого при расчете рамы Iн/Iв = 5 составило:

следовательно, статический расчет рамы уточнять не требуется.

Для увеличения жесткости на скручивание сквозной колонны с решетками в двух плоскостях при делении колонны на отправочные элементы последние укрепляются диафрагмами, расположенными у концов отправочного элемента. Диафрагмы принимаются в виде швеллера при b £ 600 мм и двутавра при b > 600 мм (рис. 8.6).

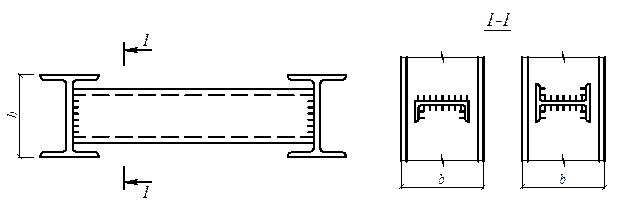
Рис. 8.6. Устройство диафрагм