Подбор сечения балки

Из условия общей прочности определяем требуемый момент сопротивления относительно оси x-x:

Wx, А = Мxβ/(Ryγc) = 389090 ∙ 1,1 / (24 ∙ 1) = 17833,3 см3,

где    β – коэффициент, учитывающий долю нормальных напряжений от горизонтальных сил:

β = 1+ МyWx,А/(МxWy,А) ≈ 1 + 2 Мyhb/(МxhТ) =

= 1 + 2 ∙136,15 ∙1,7 / (3890,9 ∙1,25) = 1,1,

здесь hТ – ширина сечения тормозной конструкции, принимаемая равной высоте сечения нижней подкрановой части колонны: hТ  = hн = 1250 мм;

hb = 1700 мм – высота балки, предварительно принимаемая в пределах (1/6 – 1/9) l (см табл. 6.3) (большие значения принимаются при большей грузоподъемности крана);

l = 12 м – пролет балки, равный шагу колонн B.

Определяем высоту балки из условия оптимального расхода стали, задаваясь гибкостью стенки kw = hw/tw = 125 при hb = 1700 мм (см. табл. 9.1):

Таблица 9.1

Практические значения kw 

Проверка жесткости подкрановой балки выполняется на нагрузку от одного крана с коэффициентом надежности по нагрузке γf  = 1 и без учета коэффициента динамичности.

Величина равнодействующей четырех сил, действующих на балку от одного крана (рис. 9.1, г):

R1 = 2Fkn1 + 2Fkn2 = 2 ∙ 450 + 2 ∙ 480 = 1860 кН.

Находим положение равнодействующей R1:

x = /R1 = / 1860 = 2 м.

Опорные реакции:

Fаn = R (6 – 1)/12 = 1860 ∙ 5 / 12 = 775 кН;

Fbn = R – Fаn = 1860 – 775 = 1085 кН.

Максимальный изгибающий момент

Мn,max = Fаn(4,2 + 0,8) – Fkn2 ∙ 0,8 = 775 ∙ 5 – 480 ∙ 0,8 = 3491 кН∙м.

Расчетное значение нормативного изгибающего момента

Мn = αМn,max = 1,05 ∙ 3491 = 3665,55 кН∙м.

Из условия жесткости, при полном использовании материала балки при загружении расчетной нагрузкой, высота балки равна:

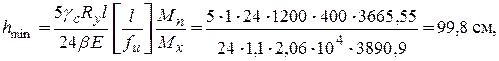
где    fu = 1/400l – предельно допустимый прогиб подкрановой балки, установленный из условия обеспечения нормальной эксплуатации кранов режимов работы 1К – 6К;  fu = 1/500l – для 7К; fu = 1/600l – для 8К.

Окончательно высоту балки принимают с учетом ширины листов (с припуском для строжки кромок) или в целях унификации конструкций – кратно 100 мм.

Принимаем hb = 1500 мм и назначаем высоту стенки hw = 1460 мм, задаваясь толщиной полок tf  = 20 мм.

Определяем минимальную толщину стенки из условия ее прочности на срез на опоре от расчетной поперечной силы:

tw = 1,5Qx/(hwRsγc) = 1,5 · 1677,5 / (146 · 13,92 · 1) = 1,29 см,

где Rs = 0,58Ry = 13,92 кН/см2.

Принимаем tw = 14 мм.

Проверяем необходимость постановки продольных ребер жесткости.

Условная гибкость стенки

следовательно, продольные ребра жесткости не требуются.

Определяем требуемые геометрические характеристики сечения:

– момент инерции сечения балки

– момент инерции стенки балки

– момент инерции поясов балки

– площадь сечения одного пояса

Af = If / = 974407,5 / = 88,97 см2;

– ширина пояса

Учитывая ослабления верхнего пояса балки двумя отверстиями             do = 23 мм под болты d = 20 мм для крепления подкранового рельса, ширину пояса принимаем несколько большей:

bf  = 445 + 2 ∙ 23 = 491 мм.

По сортаменту принимаем пояс из листа 500×20 мм (см. табл. 3.9).

Состав сечения тормозной балки: швеллер № 30 с площадью сечения       Аш = 40,5 см2, моментом инерции I1 = 327 см4, zo = 2,55 см; горизонтальный лист из рифленой стали 1050×6 мм с площадью сечения Ал = 63 см2; верхний пояс балки 500×20 мм с площадями сечения брутто Аf  = 100 см2 и нетто    Af,n = 90,8 см2.

Сечения подкрановой конструкции представлено на рис. 9.3.

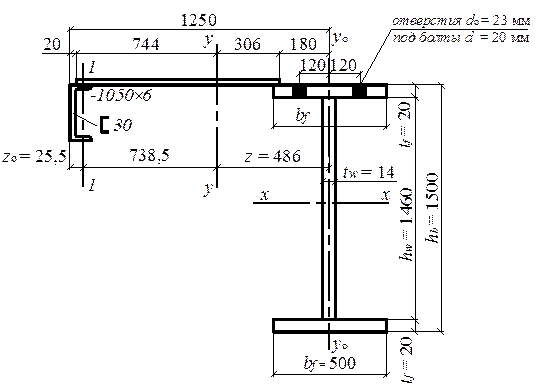
Рис. 9.3