Формирование дождевого стока

Рассмотрим бассейн стока площадью F, на который выпадает дождь (см. рис). Точка А – наиболее удаленная точка бассейна стока. При выпадении дождя стоки достигают точки Б, образуя линии равного времени добегания воды (изохроны). За 1 минуту точки Б достигают стоки с площади 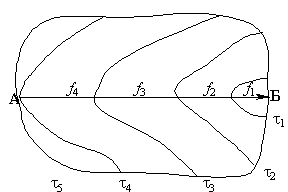f1, за вторую f2 и т.д.

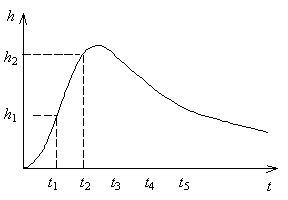
Толщина слоя осадка на площади постепенно изменяется по зависимости на графике. Расход в точке Б по истечении 1-й минуты будет: Q1 = f1h1,
за вторую минуту: Q2 = f1h2 + f2h1,
за третью: Q3 = f1h3 + f2h2 + f3h1 и т.д.

Путем интегрирования расхода получается формула для любого времени T:

,

где it – интенсивность дождя.

Эта формула применима, если T меньше времени добегания воды от точки А (τc).

При T > τc:

.

Наконец, когда дождь кончился, формула стока примет следующий вид:

,

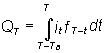где Tд – продолжительность дождя.

Если площади f равномерно возрастают, т.е. f = F/τc, то максимальный расход будет равен произведению площади стока на среднюю интенсивность дождя при продолжительности t = τc:

,