ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ - Коллоидная химия - Конспект лекций

Первое начало термодинамики представляет собой закон сохранения энергии, один из всеобщих законов природы (наряду с законами сохранения импульса, заряда и симметрии):

Энергия неуничтожаема и несотворяема; она может только переходить из одной формы в другую в эквивалентных соотношениях.

Первое начало термодинамики представляет собой постулат – оно не может быть доказано логическим путем или выведено из каких-либо более общих положений. Истинность этого постулата подтверждается тем, что ни одно из его следствий не находится в противоречии с опытом. Приведем еще некоторые формулировки первого начала термодинамики:

Полная энергия изолированной системы постоянна;

Невозможен вечный двигатель первого рода (двигатель, совершающий работу без затраты энергии).

Первое начало термодинамики устанавливает соотношение между теплотой Q, работой А и изменением внутренней энергии системы ΔU:

Изменение внутренней энергии системы равно количеству сообщенной системе теплоты минус количество работы, совершенной системой против внешних сил.

            (I.1)

          (I.2)

Уравнение (I.1) является математической записью 1-го начала термодинамики для конечного, уравнение (I.2) – для бесконечно малого изменения состояния системы.

Внутренняя энергия является функцией состояния; это означает, что изменение внутренней энергии ΔU не зависит от пути перехода системы из состояния 1 в состояние 2 и равно разности величин внутренней энергии U2 и U1 в этих состояниях:

           (I.3)

Следует отметить, что определить абсолютное значение внутренней энергии системы невозможно; термодинамику интересует лишь изменение внутренней энергии в ходе какого-либо процесса.

Рассмотрим приложение первого начала термодинамики для определения работы, совершаемой системой при различных термодинамических процессах (мы будем рассматривать простейший случай – работу расширения идеального газа).

Изохорный процесс (V = const; ΔV = 0).

Поскольку работа расширения равна произведению давления и изменения объема, для изохорного процесса получаем:

            (I.1)

           (I.4)

              (I.5)

Изотермический процесс (Т = const).

Из уравнения состояния одного моля идеального газа получаем:

             (I.6)

Отсюда:

      (I.7)

Проинтегрировав выражение (I.6) от V1 до V2, получим

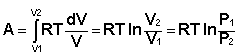        (I.8)

Изобарный процесс (Р = const).

            (I.9)

Подставляя полученные выражения для работы различных процессов в уравнение (I.1), для тепловых эффектов этих процессов получим:

                      (I.10)

     (I.11)

                (I.12)

В уравнении (I.12) сгруппируем переменные с одинаковыми индексами. Получаем:

          (I.13)

Введем новую функцию состояния системы – энтальпию H, тождественно равную сумме внутренней энергии и произведения давления на объем:

Тогда выражение (I.13) преобразуется к следующему виду:

        (I.14)

Т.о., тепловой эффект изобарного процесса равен изменению энтальпии системы.

Адиабатический процесс (Q = 0).

При адиабатическом процессе работа расширения совершается за счёт уменьшения внутренней энергии газа:

           (I.15)

В случае если Cv не зависит от температуры (что справедливо для многих реальных газов), работа, произведённая газом при его адиабатическом расширении, прямо пропорциональна разности температур:

           (I.16)