Закон уплотнения. Компрессионная зависимость, Определение модуля деформации грунта в одометре.

Бесконечно малое изменение относительного объема пор грунта прямо пропорционально бесконечно малому изменению давления:

de=-modP

Испытание грунта в приборе трёхосного сжатия ближе отвечает его работе в природных условиях и дает наиболее надежные результаты в определении его прочностных и деформационных свойств.

Поскольку уравнение (2.3) описывает изменение коэффициента пористости ei лишь в пределах секущей АВ (см. рис. 2.2, б), оно дает приближенную зависимость между коэффициентом пористости и давлением. Для большого диапазона изменения давления компрессионная кривая первичного сжатия (прямая CD на рис. 2.3,6) описывается логарифмической зависимостью

(2.5)

где ei — коэффициент пористости при давлении pi; е0 — начальный коэффициент пористости грунта; Сс — коэффициент компрессии (параметр кривой); р0 — давление, при котором начинается первичное сжатие грунта.
Продифференцировав выражение (2.5), получим
de=- Ck dp/p,
где Ck —постоянная величина.
Следовательно, при первичном сжатии изменение коэффициента пористости грунта прямо пропорционально изменению давления и обратно пропорционально суммарному давлению. Эту зависимость применяют либо при рассмотрении деформаций очень слабых грунтов, либо при изменении давления в значительных пределах.
Давление в грунте основания промышленных и гражданских зданий и сооружений обычно изменяется в небольших пределах. Чаще всего оно повышается не более чем до 0,3 МПа и в редких случаях до 0,6 МПа. При таких давлениях секущая АВ (см. рис. 2.2, б) близка к кривой, т. е. для расчетов можно пользоваться уравнением (2.3). Продифференцировав его, получим
de =- m0 dp. (2.3')
Поэтому закон компрессии грунта формулируется так: изменение коэффициента пористости грунта прямо пропорционально изменению давления.

   Компрессионная зависимость характеризует:

  - коэффициент сжимаемости грунтов mо=tgα

  - коэффициент относительной сжимаемости  mυ=mo/(1+eo)

Общий случай компрессионной зависимости характеризуется:

- σx=σy

- σz=p

- εx=0

Θ=σx+σy+σz=p(1+2ξο)

Возьмем образец грунта 6 (рис. 2.1), полностью насыщенного водой, и поместим его в кольцо 4 (высотой h) одометра. Кольцо поставим на фильтрующее днище 5 и установим поршень 2 с отверстиями. Одометр поместим в ванночку 3 с водой 1 для исключения капиллярного давления и предотвращения высыхания образца грунта. Когда грунт насыщен водой не полностью, одометр не заливают водой, а окружают влажным пористым материалом, чтобы вода не испарялась из образца. Если к поршню одометра приложить давление р, высота образца уменьшится вследствие уплотнения грунта (уменьшения его пористости). При увеличении давления образец получит дополнительное уплотнение из-за изменения объема пор.

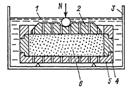
Рис. 2.1. Схема испытания образца грунта на сжатие в одометре

Одометр  прибор, служащий для определения сжимаемости грунта. Деформации в одометре возможны только в вертикальном направлении, горизонтальные деформации отсутствуют. Вертикальное напряжение изменяется ступенями и является известным, боковые напряжения реактивные и остаются неизвестными. Деформации измеряются в зависимости от усилия, приложенного на штамп. На рис. М.4.2. показана схема одометра.

Поскольку образец грунта в кольце не может иметь бокового расширения, изменение его пористости Δni под давлением pi, распределенным по площади A, найдем из выражения
Δni = siA/hA = si/h,    (2.1)
где si— осадка от давления pi
Объем твердых частиц в образце грунта до и после деформации остается практически неизменным, так как действующие напряжения не могут ощутимо изменить объем минеральных частиц. Согласно выражению (1.5), объем твердых частиц в единице объема образца грунта составляет:
m=1/(1 + е0),    (1.5')
где е0 — начальный коэффициент пористости грунта.
Делением формулы (2.1) на выражение (1.5') получим изменение коэффициента пористости образца грунта Δei под действием давления pi
Δei=(1 + е0)si/h.
Исключив значение Δei из начального коэффициента пористости e0, найдем ei — коэффициент пористости грунта при давлении pi:
ei=e0 - (1 + e0)si/h.    (2.1')
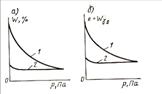
По значениям ei для различных давлений построим кривую е—р (рис. 2.2, а). Для грунтов, не обладающих структурной прочностью, получим компрессионную кривую — ветвь сжатия l. Если теперь разгружать образец грунта, уменьшая давление ступенями, то будет наблюдаться обратный процесс — увеличение объема (набухание). При этом поршень одометра переместиться вверх. Зная величину перемещения и руководствуясь формулой (2.1'), можно построить ветвь набухания 2.
Кривую зависимости коэффициента пористости от давления называют компрессионной кривой, так как она характеризует сжимаемость грунта. Закономерность изменения коэффициента пористости е, установленная К. Терцаги, развита многими советскими учеными (Н. М. Герсевановым, Н. А. Цытовичем, Н. Н. Масловым, М. Н. Гольдштейном и др.).

Расположение ветви набухания намного ниже ветви сжатия свидетельствует о том, что грунт обладает значительной остаточной деформацией уплотнения. Ветвь набухания соответствует упругим деформациям грунта и деформациям упругого последействия. Процесс набухания протекает продолжительное время, так как вода медленно входит в поры грунта под всасывающим действием скелета, стремящегося занять первоначальный объем, и расклинивающим действием молекул воды, проникающих между частицами. После снятия всей нагрузки образец грунта не может занять первоначального объема вследствие происшедших при уплотнении грунта взаимных смещений частиц, их разрушения (особенно в точках контактов) и установления новых связей между частицами при более плотном состоянии грунта (в результате сближения частиц при уплотнении).