Теоретические, фактические и расчетные эпюры напряжений под подошвой жестких фундаментов (контактная задача).

Решения Буссинеску для круглого жёсткого штампа

Контактным называют давление по подошве фундамента

Для определения контактного напряжения совместно решается два уравнения:

- Дифференциальное уравнение изогнутой оси балки;

-    Физическое уравнение связей между действующим давлением и осадкой.

-    EбJб(d4s/dx4)=qxpx;

где:  EбJб-жесткость балки

S – прогиб балки

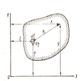
Распределение напряжений на подошве фундамента
(Контактная задача)

Этот вопрос имеет особое значение для гибких фундаментов, рассчитываемых на изгиб.

Если известно Рконт, то загружая этой величиной фундамент, можно легко определять усилия в конструкции тела фундамента.

Из курса сопротивления материалов известно, что напряжения для сжатых конструкций при прямолинейной эпюре определяются по обобщенной формуле:

smax, min =(N/F) +-(M/W)    - но здесь не учитывается работа сжимаемого основания.

Аналитическое решение по определению значений величин контактных напряжений, получено Буссинеску в виде зависимости:

Расчётная схема для решения задачи Буссинеску.

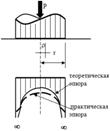Анализируя аналитическую зависимость (см. приведённую выше формулу и схему), можно записать, что

При ρ = r → Рρ = ∞

При ρ = 0 → Рρ = 0,5Рср

и построить теоретическую эпюру контактных напряжений. Фактически же, грунт под подошвой фундамента, при давлениях, стремящихся к бесконечности (краевые точки) разрушаясь, приводит к перераспределению напряжений, возникает практическая эпюра (см. приведенную схему). Однако в данной методике также не учитываются свойства грунта основания.

При дальнейших исследованиях было установлено, что эпюра контактных напряжений под подошвой фундамента будет зависеть от его гибкости (Г) - обобщённой характеристики, учитывающей деформативные свойства основания.

Р = f(Г)

Понятие гибкости (Г) было введено профессором Горбуновым-Посадовым М.И.

Е0 – модуль деформации грунта;

ℓ – полудлина фундамента (балки);

Е1 – модуль упругости материала фундамента;

h1 – высота фундамента.

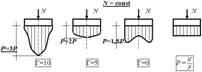
Эпюры контактных напряжений под подошвой фундамента в зависимости от его гибкости. Крайняя правая схема на данном рисунке показывает, что для абсолютно жёстких фундаментов (Г=0), в целях аппроксимации, принята не фактическая седлообразная эпюра контактных напряжений, а прямоугольная (использование аппарата теории упругости к грунтам).

Форма эпюры контактных напряжений зависит и от ширины подошвы фундамента Р = f(b) и при прочих равных условиях (mv – const; N – const) и может быть представлена на следующей схеме:

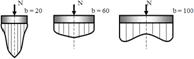
Эпюры контактных напряжений под подошвой фундамента в зависимости от его ширины.

Форма эпюры контактных давлений зависит и от степени нагружения фундамента Р = f (N) и при прочих равных условиях (mv – const; F - const) может быть представлена на следующей схеме:

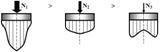
Эпюры контактных напряжений под подошвой фундамента в зависимости от степени нагружения.

Таким образом, приведённые примеры дают наглядную картину изменения величины и формы эпюры контактных напряжений в зависимости от поэтапного нагружения (увеличение веса сооружения в процессе его строительства), что значительно осложняет решение поставленной задачи.