Применение теории предельного равновесия к решению задач об устойчивости откосов, фундаментов и сооружений.

Реальные грунты, как правило, обладают не только сцеплением, но и трением. В связи с этим проблема устойчивости откосов становится значительно сложнее.

Теория предельного равновесия грунтов, развитая В.В. Соколовским, позволяет решать задачи двух типов:

-задан угол наклона плоского откоса, определяется интенсивность
внешней нагрузки на верхней горизонтальной поверхности грунта, офаниченного откосом массива;

-задана интенсивность нагрузки на верхней горизонтальной поверхности грунта, офаниченного откосом массива, определяется форма равноустойчивого откоса, находящегося в предельном напряженном состоянии.
Задача первого типа, при однородных грунтах и плоском откосе (рис. 1) решена В.В. Соколовским в безразмерных величинах.

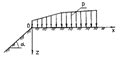
Рис. 1. Схема к расчету устойчивости плоского откоса по теории предельного равновесия

Исходными уравнениями для решения этой задачи являются:

                   (1)

                       (2)

       (3)

Выражения (1) и (2), как было выше сказано, представляют дифференциальные уравнения равновесия, а (3) — условие предельного равновесия.

Предельная нагрузка на верхней горизонтальной поверхности откоса, зная q , определяется из выражения

        (4)

где q — безразмерный коэффициент, зависящий от углов внутреннего трения φ, угла α  и расстояния х от края откоса до рассматриваемой точки).