При изучении механических колебаний было установлено, что полная энергия колебаний гармонического осциллятора W = mω2A2/2 , где А — амплитуда колебания, (см. формулу (3.14)). Именно эта энергия переносится волной посредством возбуждения колебаний близлежащих частиц. Более полной характеристикой процесса переноса энергии волной является вектор плотности потока энергии волны j , который определяет количество энергии, переносимое волной через единицу площади в одну секунду в направлении ее распространения. Если v – скорость волны, то за время Dt через площадку DS, перпендикулярную направлению распространения, переносится количество энергии:
,
где w — плотность энергии, заключенной в объеме V.
Разделив это выражение на DSDt, получим величину плотности потока энергии:
j = w×v. (3.58)
Наконец, если ввести вектор 
, равный по величине фазовой скорости волны и направленный вдоль волнового вектора 
(3.55), получим выражение для вектора плотности потока энергии:
. (3.59)
Следовательно, направление вектора плотности потока энергии совпадает с направлением распространения волны.
Вектор (3.59) называется вектором Умова-Пойнтинга. Он является важной характеристикой переноса энергии волной я сохраняет свое значение и в тех случаях, когда речь идет не только о колебаниях частиц, но и о волновом процессе изменения любых физических величин, например температуры, электрического или магнитного полей.
Необычное перераспределение энергии колебаний происходит при наложении двух волн, бегущих навстречу друг другу, в том случае, когда разность фаз между волнами в процессе распространения волн остается постоянной. Такая ситуация реализуется при отражении бегущей волны от препятствия, например, при возбуждении упругой волны в струне, один из концов которой закреплен. При этом возникает отраженная волна, бегущая навстречу первой. Пусть для простоты начальные фазы обеих волн равны нулю. Тогда результирующая волна будет суммой двух волн, бегущих в противоположных направлениях:
u1 = u0 cos(ωt – kx), u0 = u0 cos(ωt + kx). (3.60)
Сложив эти уравнения и преобразовав результат сложения по формуле для суммы косинусов, получим:
u = u1 + u0 = 2u0cos kx×cos ωt. (3.61)
Заметим, что в результате наложения волн характер колебаний существенно изменился. Колебания во всех точках происходят одновременно с одинаковой частотой ω. Иными словами, вся система колеблется как целое, причем передачи энергии в процессе колебаний от одной точки к другой не происходит. Каждая частица колеблется так, как это происходит при обычных колебаниях — в момент времени, когда ее смещение максимально, максимальна ее потенциальная энергия и минимальна кинетическая, и наоборот. В каждый момент времени система частиц образует в пространстве периодическую структуру, форма которой определяется амплитудным множителем в выражении (3.61):
A(x) = 2u0 coskx. В точках x = ±2nl/4 (n = 0, 1, 2,..) (3.62)
амплитуда колебаний наибольшая, а в точках
x=±(2n+1)l/4 (3.63)
она равна нулю. Эти точки называют соответственно пучностями и узлами волны. Узлы и пучности волны расположены друг от друга на расстоянии l/4.
Описанную картину колебаний во встречных бегущих волнах называют стоячей волной. Ясно, что в замкнутом объеме, где бегущая волна испытывает отражение от обеих границ, устанавливается стоячая волна.
Колебания струны (стержня).
В натянутой струне, закрепленной с обоих концов, при возбуждении какого-либо произвольного поперечного возмущения возникнет довольно сложное нестационарное движение. Стационарное же движение в виде стоячей волны возможно лишь при вполне определенных частотах. Это связано с тем, что на закрепленных концах струны должны выполняться определенные граничные условия: в них смещение u все время должно равняться нулю. Значит, если в струне возбуждается стоячая волна, то концы струны должны быть ее узлами. Отсюда следует, что на длине струны l должно укладываться целое число п полуволн: l = n∙λ/2. Из этого условия находим возможные длины волн:
ln = 2l/n, n = 1,2,...Соответствующие частоты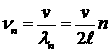 
,
где v — фазовая скорость волны, определяемая, согласно (1.30), силой F натяжения струны и линейной плотностью ρ т. е. массой единицы ее длины.
Частоты νn называют собственными частотами струны. Частоту ν1 (n=1) называют основной частотой, остальные ν2, ν3, ... — обертонами. Гармонические колебания с частотами (1.57) называют собственными колебаниями, или гармониками. В общем случае колебания струны представляют собой суперпозицию различных гармоник (спектр).
Колебания струны примечательны тем, что в рамках классической физики возникает дискретный спектр одной из величин (частоты). Такая дискретность для классической физики является исключением, в отличие от квантовой физики.
Приведенные выше соображения относятся не только к струне, но и к стержням, закрепленным различным образом — в середине, на одном конце и т. д. Отличие заключается лишь в том, что свободный конец стержня является пучностью. Это касается как поперечных, так и продольных колебаний.
Пример. Найдем собственные частоты стержня, закрепленного на одном конце, если длина стержня l, модуль Юнга материала стержня E и его плотность ρ.
Поскольку свободный конец стержня должен быть пучностью, на длине стержня установится целое число полуволн и еще четверть волны, т. е. l = nλ/2 + λ/4 = (2n + 1)λ/4. Отсюда найдем возможные значения λn, а затем, учитывая (1.26), и собственные частоты:
, n=0,1,2,...
Эффект Доплера для звуковых волн
Пусть источник, находящийся в газе или жидкости, испускает короткие импульсы с частотой ν. Если источник и приемник покоятся относительно среды, в которой распространяется волна, то частота воспринимаемых приемником импульсов будет равна частоте ν источника. Если же источник, или приемник, или оба движутся относительно среды, то частота ν', воспринимаемая приемником, вообще говоря, оказывается отличной от частоты источника: ν' ¹ ν. Это явление называют эффектом Доплера.
Сначала рассмотрим случай, когда источник S и приемник P движутся вдоль проходящей через них прямой с постоянными скоростями u и u' соответственно (относительно среды).
Если бы двигался только источник навстречу приемнику, испуская импульсы с периодом T = 1/ν, то за это время очередной импульс пройдет относительно среды расстояние λ = v∙T, где v — скорость волн в среде, и пока будет испущен следующий импульс, источ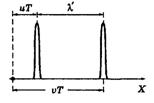
ник «нагонит» предыдущий импульс на расстояние uT. Таким образом, расстояние между импульсами в среде станет равным λ' = vT – uT
(рис.), и воспринимаемая неподвижным приемником частота (число импульсов за единицу времени)
.
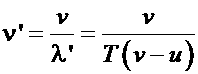Если же движется и приемник (пусть тоже навстречу источнику, то импульсы относительно приемника будут иметь скорость v + u', и число воспринимаемых за единицу времени импульсов
.
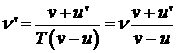Нетрудно сообразить, что при движении как источника, так и приемника в противоположных направлениях, знаки перед u' и u надо поменять на обратные. Еще раз подчеркнем, что скорости u' и u — это скорости приемника и источника относительно среды.
Как видно из приведенных рассуждений, эффект Доплера является следствием «уплотнения» (или разряжения) импульсов, обусловленным движением источника и приемника.
Формулу целесообразнее записать в иной форме, более общей и более простой для запоминания и использования:
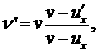
u'x и ux – проекции скоростей приемника и источника на ось X, проходящую через них и положительное направление которой совпадает с направлением распространения импульсов, т. е. от источника S к приемнику P.
Прежде чем продолжить обсуждение возможностей выражения (1.60), приведем два простых примера.
Пример 1. Источник S и приемник P удаляются друг от друга по одной прямой в противоположные стороны относительно среды со скоростями u и u'. Частота источника ν, скорость сигналов в среде v. Найдем частоту v', воспринимаемую приемником.
В данном случае проекция скорости приемника на ось X есть u'х = u', а проекция скорости источника ux = -u. Подставив эти величины в формулу (1.60), получим
ν' = ν (v - u')/(v + u).
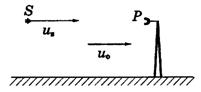Пример 2. Источник S, испускающий сигналы с частотой ν, движется с постоянной скоростью us
относительно приемника P, установленного на башне (рис.). При этом воздушная масса перемещается относительно земной поверхности вправо с постоянной скоростью u0 (ветер). Скорость звука в воздухе v. Найдем частоту v', воспринимаемую приемником.
Имея в виду, что в формулу входят скорости относительно среды, запишем: проекция скорости приемника u'х = – u0, а проекция скорости источника uх = us – u0. Обе проекции взяты, как должно быть, на ось X, направленную вправо. Остается подставить эти проекции в формулу (1.60), и мы получим:
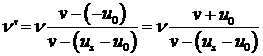
Поможем написать любую работу на аналогичную тему