Равновесные процессы в идеальном газе - Шпаргалки по Физике

Если макроскопические параметры системы имеют одинаковые значения во всем объеме, занимаемом системой, и не изменяются с течением времени, то состояние системы является равновесным. Последовательный переход системы из одного равновесного состояния в другое, совершаемый достаточно медленно, так, что в любой заданный момент времени систему можно характеризовать определенными равновесными значениями термодинамических параметров: давления, температуры или объема, называется равновесным процессом.

Равновесный процесс представляет собой приближенную модель реального термодинамического процесса. Рассмотрим, например, сжатие газа поршнем в закрытом сосуде. Если поршень вдвигать достаточно быстро, то давление поршня на газ не будет успевать распространяться по всему объему, занятому газом. Давление газа на поршень в каждый момент времени будет больше, чем давление газа на стенки сосуда. Состояние газа в этом случае нельзя характеризовать определенной величиной давления, оно будет существенно неравновесным. Со временем давление перераспределится по всему объему и состояние газа станет равновесным с новым значением давления. Время установления нового состояния равновесия газа определяется его плотностью и температурой. Процесс установления термодинамического равновесия в системе носит название релаксационного процесса, а время установления равновесия — времени релаксации.

В случае, когда газ под действием поршня сжимается достаточно медленно, давление успевает равномерно распределиться по всему объему, и в газе в любой заданный момент времени устанавливается равновесие. Таким образом, при медленном движении поршня газ проходит последовательно через ряд равновесных состояний, и процесс термодинамически равновесный. Для того чтобы процесс был равновесным, очевидно, необходимо, чтобы время релаксации в системе было меньше времени, в течение которого система подвергается внешнему возмущению.

Рассмотрим ряд равновесных процессов в идеальном газе, имеющих важное значение в термодинамике. При равновесных процессах термодинамические параметры P, V и T в каждый момент времени связаны между собой уравнением состояния (2.8).

1) Изотермический процесс.

При изотермическом процессе температура газа остается постоянной в течение всего процесса. Уравнение состояния газа в этом случае имеет вид:

.                                                   (2.37)

При заданной температуре состояние газа изображается точкой на плоскости, где по осям отложены давление и объем. Последовательность таких точек образует кривую, представляющую изотермический процесс. В случае изотермического процесса кривая является гиперболой и называется изотермой. Разным температурам газа соответствуют различные изотермы.

Вычислим работу, производимую газом при изотермическом процессе. Поскольку температура газа остается постоянной dT = 0, при термодинамическом процессе не изменяется внутренняя энергия газа, dE=0, т.е. все подводимое в систему тепло расходуется только на совершение механической работы dQ = PdV. Таким образом,

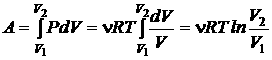.                      (2.38)

При изотермическом сжатии газа механическая работа, совершаемая над системой, переходит в тепловую энергию окружающих тел.

2) Изобарический процесс.

Этот термодинамический процесс происходит при постоянном давлении. Ему соответствуют на диаграмме P,V горизонтальные прямые — изобары, определяемые уравнением состояния:

.                                   (2.39)

Работа при изобарическом процессе пропорциональна разности объемов газа в начальном и конечном состояниях:

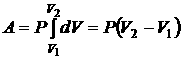.                              (2.40)

3) Изохорический процесс.

Зависимость давления от температуры при постоянном объеме представляет собой в координатах P, V вертикальную прямую, называемую изохорой. Поскольку при этом процессе dV = 0, работа равна нулю.

4) Адиабатический процесс происходит в системе без теплообмена с окружающей средой, т. е. dQ = 0. Из первого начала термодинамики (2.32) следует, что при таком процессе dE = ‑ Pd V , т. е. изменение внутренней энергии системы происходит только за счет совершения работы. Выразим изменение внутренней энергии через теплоемкость при постоянном объеме согласно формуле (2.34): dE = v·CV·dT .Тогда

v·CV·dT = ‑ PdV.                                          (2.41)

Отсюда следует, что при адиабатическом расширении газа dV > 0,  dT < 0, и газ охлаждается. При сжатии газа, наоборот, происходит его нагревание и соответственно увеличение внутренней энергии.

Разделив выражение (2.41) соответственно на правую и левую части уравнения состояния v·R·T = P·V , интегрируя это соотношение, получим

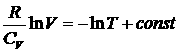
Наконец, воспользовавшись связью между CP и CV (2.36) в виде R = CP ‑ CV и вводя определенную ранее характерную для газа величину 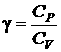, получим окончательное соотношение между давлением и объемом идеального газа при адиабатическом процессе

.                                                        (2.42)

 Полученное уравнение называется уравнением адиабаты. На плоскости P, V она изображается кривой, которая спадает более круто, чем изотерма (γ > 1).

Работа при адиабатическом процессе пропорциональна изменению температур газа в начальном и конечном состояниях:

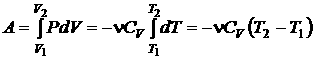.          (2.43)

Все указанные процессы можно рассматривать как частные случаи общего более сложного процесса, при котором давление и объем связаны уравнением

.                                                        (2.44)

При n = 0 уравнение описывает изобару, при n = 1 — изотерму, при n = γ —адиабату та. при n = ∞ — изохору. Реальный неидеализированный процесс соответствует промежуточным значениям показателя степени в уравнении (2.44).