Начала статистической физики: эргодическая гипотеза, статистический вес, статистическое толкование энтропии.

Пусть наша система состоит из одной частицы. Мы следим за скоростью частицы. Естественно нас интересует средняя скорость частицы:

.

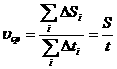 Эргодическая гипотеза утверждает, что такая средняя скорость равняется средней скорости, вычисленной по ансамблю систем, т.е. среднее значение величины, вычисленное по времени равняется среднему значению величины, вычисленному по ансамблю систем.Пусть число систем в ансамбле , в некоторый момент времени :

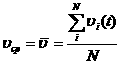
Впервые эта гипотеза была высказана в 1871 г. Л. Больцманом (1844-1906). Затем Дж. Максвелл в 1879 г. проанализировал возможность замены средних значений по времени средними значениями по ансамблю. Используя эту гипотезу, мы можем вопрос об изучении параметров системы, меняющихся со временем, свести к одномоментному усреднению по ансамблю!

Статистический вес Г: определяется числом микросостояний, реализующих данное макросостояние. Причем справедлив постулат равновероятности всех микросостояний.

Общее число микросостояний равно, очевидно, числу способов, которыми можно разместить  частиц по  ячейкам, где - объем занимаемый системой из  частиц. Конкретную формулу дает комбинаторика. Отметим, что статистический вес для моля кислорода при нормальном атмосферном давлении  и комнатной температуре 20°С

Статистический вес Г еще называют термодинамической вероятностью состояния системы. Т.к. это число способов, которыми может быть реализовано данное макросостояние системы, по определению, . Таким образом, термодинамическая вероятность не есть вероятность в математическом смысле (т.к. ).

Будем отличать макросостояния номерами ,  - статистический вес  -го макросостояния.

Используя это понятие, Больцман в 1872 г. Предложил статистическое толкование энтропии. Это более глубокое толкование.

Согласно Больцману, энтропия системы и статистический вес Г связаны между собой соотношением

                  или                      и

 - если система состоит из подсистем с .

Она определяется логарифмом числа микросостояний, с помощью которых было реализовано данное макросостояние.

Тогда  статистический вес системы выражается через произведение  подсистем.

Следовательно, энтропия может рассматриваться как мера вероятности состояния  термодинамической системы.

Формула Больцмана позволяет дать энтропии следующее определение (статистическое толкование).

Энтропия является мерой неупорядоченности системы. Энтропия есть количественная мера беспорядка системы многих частиц.

В самом деле, чем больше число микросостояний реализующих данное макросостояние, тем больше энтропия.

В изолированной ТЕРМОДИНАМИКИ системе все процессы идут в направлении возрастания энтропии, в направлении наиболее вероятного макросостояния (равновесного). Энтропия возрастает по II началу ТЕРМОДИНАМИКИ, следовательно, естественные процессы стремятся перевести систему в состояние с наибольшим беспорядком. Это тенденция, хотя возможны отермодинамикиельные флуктуации, понижающие энтропию.