Вывод основного уравнения молекулярно-кинетической теории идеального газа.

Применим распределение Максвелла для вывода основного уравнения кинетической теории  газов. Наша задача установить путем статистического усреднения микрохарактеристик молекул системы,  некоторые  макрохарактеристики, описывающие газ в целом. Известно, что давление газа создается за счет ударов молекул газа о стенки сосуда. Примем, что удар является абсолютно упругим и молекулы бомбардируют стенки как материальные точки под разными углами и с различными скоростями.

По второму закону Ньютона: , .

Молекулы ударяются о стенку и отскакивают, меняя только -составляющую скорости. Подсчитаем изменение -составляющей импульса всех молекул за время . Надо подсчитать поток импульса молекул в  положительном направлении оси , т.е. м2, с, поток – число частиц пролетающих за единицу времени через единичную площадку. В стенку ударятся только те молекулы, которые движутся к ней, а не от нее, т.е. . За время  до стенки долетают все молекулы в объеме , .

Вероятность частиц иметь такую скорость , тогда число частиц, имеющих такую скорость .

Импульс, передаваемый стенке сосуда

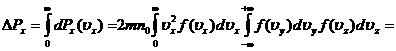, вычислим  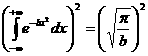  отермодинамикиельно внутренний интеграл и подставим в выражение

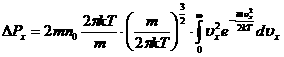, рассчитаем интеграл, сделав замену переменной,

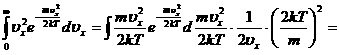
  , ,  , отсюда , ,   , , , подставим полученное  в интеграл:

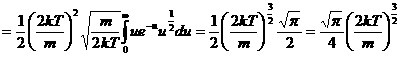.  Таким образом давление на стенку

.

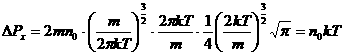Аналогично для других стенок , с другой стороны , тогда
, таким образом ,  - основное уравнение молекулярно-кинетической теории идеального газа.

Отсюда можно получить уравнение состояния идеального газа:

 Þ  - уравнение состояния идеального газа.