Изотермы Ван-дер-Ваальса и их анализ.
Для исследования поведения реального газа рассмотрим изотермы Ван-дер-Ваальса — кривые зависимости ![]() при заданных значениях
при заданных значениях ![]() , определяемые уравнением Ван-дер-Ваальса (2.2) для моля газа. Эти кривые (рассматриваются для четырех различных температур; рис. 89) имеют своеобразный характер. При высоких температурах (
, определяемые уравнением Ван-дер-Ваальса (2.2) для моля газа. Эти кривые (рассматриваются для четырех различных температур; рис. 89) имеют своеобразный характер. При высоких температурах (![]() ) изотерма реального газа отличается от изотермы идеального газа только некоторым искажением ее формы, оставаясь монотонно спадающей кривой. При некоторой температуре
) изотерма реального газа отличается от изотермы идеального газа только некоторым искажением ее формы, оставаясь монотонно спадающей кривой. При некоторой температуре ![]() на изотерме имеется точка перегиба
на изотерме имеется точка перегиба ![]() . Эта изотерма называется критической, соответствующая ей температура
. Эта изотерма называется критической, соответствующая ей температура ![]() — критической температурой. Критическая изотерма имеет лишь одну точку перегиба
— критической температурой. Критическая изотерма имеет лишь одну точку перегиба ![]() - называемую критической точкой; в этой точке касательная к изотерме параллельна оси абсцисс. Соответствующие этой точке объем
- называемую критической точкой; в этой точке касательная к изотерме параллельна оси абсцисс. Соответствующие этой точке объем ![]() и давление
и давление ![]() называются также критическими. Состояние с критическими параметрами (
называются также критическими. Состояние с критическими параметрами (![]() ,
,![]() ,
,![]() ) называется критическим состоянием. При низких температурах (
) называется критическим состоянием. При низких температурах (![]() ) изотермы имеют волнообразный участок, сначала монотонно опускаясь вниз, затем монотонно поднимаясь вверх и снова монотонно опускаясь.
) изотермы имеют волнообразный участок, сначала монотонно опускаясь вниз, затем монотонно поднимаясь вверх и снова монотонно опускаясь.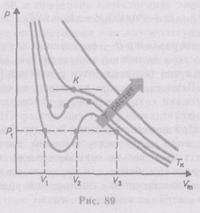
Для пояснения характера изотерм преобразуем уравнение Ван-дер-Ваальса (3) к виду:
![]() . (3.1)
. (3.1)
В таком виде уравнение, при заданных ![]() и
и ![]() , является уравнением третьей степени относительно
, является уравнением третьей степени относительно ![]() .
.
Кубическое уравнение может иметь либо три вещественных корня, либо один вещественный и два мнимых. Причем физический смысл имеют лишь вещественные положительные корни. Поэтому первому случаю соответствуют изотермы при низких температурах (три значения объема газа ![]() ,
, ![]() и
и ![]() отвечают одному значению давления
отвечают одному значению давления ![]() ), второму случаю— изотермы при высоких температурах.
), второму случаю— изотермы при высоких температурах.
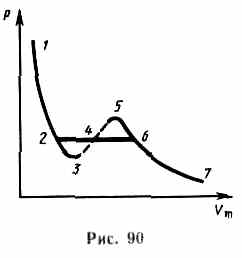 Рассматривая различные участки изотермы при
Рассматривая различные участки изотермы при ![]() (рис.90), видим:
(рис.90), видим:
на участках 1—3 и 5—7 при уменьшении объема ![]() давление
давление ![]() возрастает, что соответствует естественному поведению газа;
возрастает, что соответствует естественному поведению газа;
на участке 3—5 сжатие вещества приводит к уменьшению давления; практика показывает, что такие состояния в природе не осуществляются. Наличие участка 3—5 означает, что при постепенном изменении объема вещество не может оставаться все время в виде однородной среды; в некоторый момент должно наступить скачкообразное изменение состояния и распад вещества на две фазы.
Таким образом, истинная изотерма будет иметь вид ломаной линии 7—6—2—1.
Часть 7—6 — отвечает газообразному состоянию;
часть 2—1 — жидкому;
часть 6—2, — горизонтальный участок, соответствующий равновесию жидкой и газообразной фаз вещества.
Вещество в газообразном состоянии при температуре ниже критической называется паром, а пар, находящийся в равновесии со своей жидкостью, называется насыщенным.
Данные выводы, следующие из анализа уравнения Ван-дер-Ваальса, были подтверждены опытами ирландского ученого Т. Эндрюса (1813—1885), изучавшего изотермическое сжатие углекислого газа. Отличие экспериментальных (Эндрюс) и теоретических (Ван-дер-Ваальс) изотерм заключается в том, что превращению газа в жидкость в первом случае соответствуют горизонтальные участки, а во втором — волнообразные.
Для нахождения критических параметров подставим их значения в уравнение (3.1) и запишем для одного моля:
![]() (3.2)
(3.2)
Поскольку в критической точке все три корня совпадают и равны ![]() , уравнение приводится к виду
, уравнение приводится к виду
![]() , или
, или ![]() . (3.3)
. (3.3)
Так как уравнения (3.2) и (3.3) тождественны, то в них должны быть равны и коэффициенты при неизвестных соответствующих степеней. Поэтому можно записать:
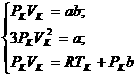 Решая полученную систему уравнений, найдем:
Решая полученную систему уравнений, найдем:
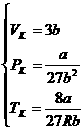 . (4)
. (4)
Если решить систему относительно постоянных величин ![]() , получаем:
, получаем:
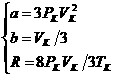 .
.
 Полученные соотношения показывают, что для каждого реального газа необходимо вычислять его индивидуальную газовую постоянную
Полученные соотношения показывают, что для каждого реального газа необходимо вычислять его индивидуальную газовую постоянную ![]() , которая отличается от молярной газовой постоянной
, которая отличается от молярной газовой постоянной ![]() причем оказывается индивидуальная газовая постоянная меньше, чем молярная. Поскольку газовая постоянная пропорциональна числу молекул в моле, заключаем, что в критическом состоянии происходит уменьшение структурных единиц, образующих газовую постоянную, т.е. молекулы объединяются в комплексы. При удалении от критического состояния эти комплексы распадаются, и индивидуальная газовая постоянная становится равной молярной.
причем оказывается индивидуальная газовая постоянная меньше, чем молярная. Поскольку газовая постоянная пропорциональна числу молекул в моле, заключаем, что в критическом состоянии происходит уменьшение структурных единиц, образующих газовую постоянную, т.е. молекулы объединяются в комплексы. При удалении от критического состояния эти комплексы распадаются, и индивидуальная газовая постоянная становится равной молярной.
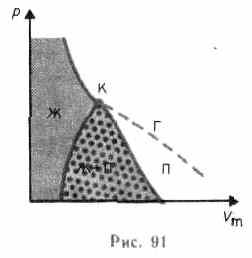
 Если через крайние точки горизонтальных участков семейства изотерм провести линию, то получится колоколообразная кривая (рис. 91), ограничивающая область двухфазных состояний вещества. Эта кривая и критическая изотерма делят диаграмму
Если через крайние точки горизонтальных участков семейства изотерм провести линию, то получится колоколообразная кривая (рис. 91), ограничивающая область двухфазных состояний вещества. Эта кривая и критическая изотерма делят диаграмму ![]() ,
, ![]() под изотермой на три области: под колоколообразной кривой располагается область двухфазных состояний (жидкость и насыщенный пар), слева от нее находится область жидкого состояния, а справа — область пара. Пар отличается от остальных газообразных состояний тем, что при изотермическом сжатии претерпевает процесс сжижения. Газ же при температуре выше критической не может быть превращен в жидкость ни при каком давлении.
под изотермой на три области: под колоколообразной кривой располагается область двухфазных состояний (жидкость и насыщенный пар), слева от нее находится область жидкого состояния, а справа — область пара. Пар отличается от остальных газообразных состояний тем, что при изотермическом сжатии претерпевает процесс сжижения. Газ же при температуре выше критической не может быть превращен в жидкость ни при каком давлении.
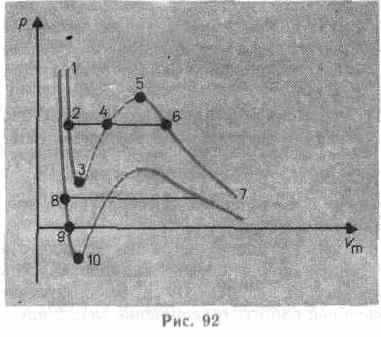
Сравнивая изотерму Ван-дер-Ваальса с изотермой Эндрюса (верхняя кривая на рис. 92), видим, что последняя имеет прямолинейный участок 2—6, соответствующий двухфазным состояниям вещества. Правда, при некоторых условиях могут быть реализованы состояния, изображаемые участками ван-дер-ваальсовой изотермы 5—6 и 2—3. Эти неустойчивые состояния называются метастабильными.
Участок 2—3 изображает перегретую жидкость,
5—6 — пересыщенный пар. Обе фазы ограниченно устойчивы.
При достаточно низких температурах изотерма пересекает ось ![]() , переходя в область отрицательных давлений (нижняя кривая на рис. 92). Вещество под отрицательным давлением находится в состоянии растяжения. При некоторых условиях такие состояния также реализуются. Участок 8—9 на нижней изотерме соответствует перегретой жидкости, участок 9— 10 — растянутой жидкости.
, переходя в область отрицательных давлений (нижняя кривая на рис. 92). Вещество под отрицательным давлением находится в состоянии растяжения. При некоторых условиях такие состояния также реализуются. Участок 8—9 на нижней изотерме соответствует перегретой жидкости, участок 9— 10 — растянутой жидкости.
Поможем написать любую работу на аналогичную тему

