Ток смещения.   - Лекции по магнетизму.

Прежде чем приступить к изучению второго уравнения Максвелла, необходимо ознакомиться с понятием тока смещения. Максвелл предположил, что если переменное магнитное поле возбуждает в окружающем его пространстве электрическое, то должно существовать и обратное явление. Всякое изменение электрического поля должно вызывать появление вихревого магнитного поля. Это определяет существование еще одного явления индукции. Только в уравнении, которое его описывает, векторы В и Е должны поменяться местами.

Пусть переменное магнитное поле создается переменным током, т.е. током, сила которого изменяется во времени по гармоническому закону:   .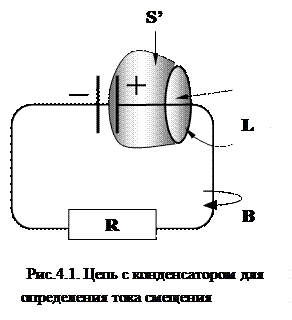

Рассмотрим цепь переменного тока, содержащую конденсатор С (рис.4.1). Пусть правая пластина конденсатора заряжена положительно, левая – отрицательно. При замыкании цепи конденсатор разряжается через сопротивление R, при этом вокруг проводника создается магнитное поле В.  Проведем вокруг провода замкнутый круговой контур L и нарисуем  две ограниченных контуром L поверхностей – S и S’ (см. рис.4.1). Поверхность S пересекает проводник с током, а S’ – не пересекает. Очевидно, что через поверхность S’, которая, как и S, проведена через контур L (и имеет с ней равные права!) тока не течет. Через поверхность S протекает ток (рис. 4.2). Максвелл заключил, что раз между обкладками заряжающегося и разряжающегося конденсатора имеется переменное магнитное поле, то между обкладками должен протекать некоторый ток, названный им током смещения.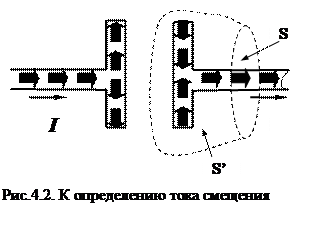 Согласно Максвеллу, токи смещения протекают в тех участках, где отсутствуют проводники. Переменное электрическое поле в конденсаторе в каждый момент времени создает такое магнитное поле, как если бы между обкладками конденсатора существовал ток смещения, равный току в подводящих проводах.

Найдем количественное соотношение для “новой индукции”, т.е. связь между переменным электрическим полеми вызываемым им магнитным полем. Если σ – поверхностная плотность зарядов на обкладке конденсатора, то заряд на ней . Ток проводимости вблизи обкладок конденсатора:

.

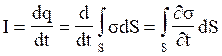Здесь мы поменяли местами операции интегрирования по поверхности и дифференцирования по времени, поскольку поверхность S неподвижна. Ранее было получено для  конденсатора  σ = D, где D – электрическое смещение в конденсаторе. Поэтому мы можем записать в векторной форме:

.

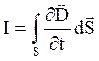Сила тока, текущего через поверхность S связана с  плотностью силы тока  j следующим образом: 

.

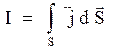Из сравнения двух последних соотношений следует 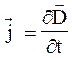 . Численное значение плотности тока обусловлено в данном случае не движением свободных электрических зарядов, а изменением во времени электрического поля. Поэтому Максвелл предложил назватьплотностью тока смещения   .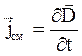

Плотность тока смещения в данной точке пространства равна скорости изменения вектора электрического смещения в этой точке.

Ток смещения сквозь произвольную поверхность S:

.

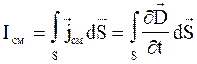Каково же направление векторов  и ?  Определим это с помощью рис.4.3.

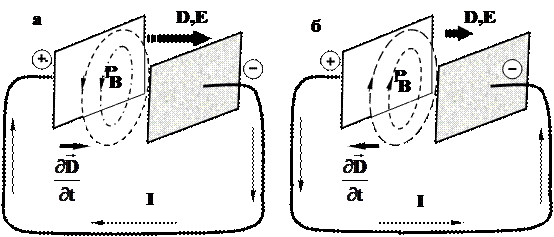На рис. 4.3 а ток изображен текущим от правой обкладки конденсатора к левой. Если конденсатор заряжается, следовательно, поле между обкладками усиливается, величина электрического смещения  увеличивается. Последнее означает, что 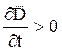, т.е. векторы  и  направлены в одну сторону.

При разрядке конденсатора (рис.4.3 б) ток начинает течь в противоположную сторону, и поле в конденсаторе ослабляется. Направление векторов  и  сохраняется, но они со временем уменьшаются по величине и теперь приращение  становится отрицательным, т.е. 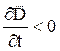. Векторы  и  направлены в противоположные стороны. Таким образом, в каждом из рассмотренных случаев направление , а следовательно, и вектор плотности тока смещения   совпадает с направлением вектора плотности тока проводимости . Ток смещения обладает способностью создавать в окружающем пространстве магнитное поле. Направление силовых линий поля (с учетом правила правой руки) показано на рис.4.3.

Ток смещения, таким образом, появляется там, где есть изменяющееся во времени электрическое поле. Поэтому он существует не только в вакууме и в диэлектриках, но и внутри проводников, по которым проходит переменный электрический ток. Однако в таких случаях он пренебрежимо мал по сравнению с током проводимости.