Закон преломления

Оптически однородная среда 1 характеризуется абсолютным показателем преломления

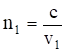                                                         ,                                                      (1.2)

где с - скорость света в вакууме;  v1 - cкорость света  в первой среде.

Среда 2  характеризуется абсолютным показателем преломления

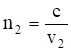                                                        ,                                                     (1.3)

где v2 - скорость света во второй среде.

Отношение 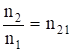                                                                                         (1.4)

называют относительным показателем преломления второй среды относительно первой.

Для прозрачных диэлектриков, у которых m=1, используя теорию Максвелла, имеем

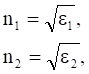                                                                                                    (1.5)

где e1,  e2 - диэлектрические проницаемости первой и второй сред.

Для вакуума n=1. Из-за дисперсии (частоты света n » 1014 Гц), например, для воды n =1,33, а  не n=9 (e=81), как это следует из электродинамики для малых частот.

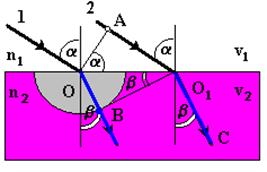
Если скорость распространения света в первой среде v1, а во второй - v2, то за время Dt прохождения падающей плоской волной расстояния  АО1 в первой среде    АО1 = v1Dt, фронт вторичной волны, возбуждаемый во второй среде (в соответствии с принципом Гюйгенса), достигает точек полусферы, радиус которой  ОВ = v2Dt.

Новый фронт волны, распространяемой во второй среде, изображается плоскостью  ВО1 (рис. 1.3), а направление ее распространения - лучами ОВ и О1С (перпендикулярными к фронту волны).

Угол b между лучом ОВ и нормалью к границе раздела двух диэлектриков в точке О называют углом преломления.

Из треугольников ОАО1   и  ОВО1 следует,  что    АО1 = ОО1 sin a,   OB = OO1 sin b.

Их отношение и выражает закон преломления (закон Снеллиуса):

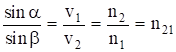      .     (1.6)

Отношение синуса угла падения к синусу угла преломления равно относительному показателю преломления двух сред.         

                        Рис. 1.3