Статистические методы психогенетики. Коэффициенты наследуемости Хольцингера, Игнатьева. Анализ путей.

Образно говоря, статистика является «правой рукой» психогенетики. Как уже отмечалось, психогенетика изучает вопросы наследования поведенческих признаков и психологических функций в популяциях, и по определению эта наука озабочена не отдельными индивидуальностями, а их разнообразием, т.е. популяционной изменчивостью (вариативностью, дисперсией) изучаемого признака. Иными словами, психогенетику интересуют вопросы, касающиеся характеристик распределений (среднего, дисперсии и других моментов распределения) индивидуальных значений по изучаемому признаку в популяции, а также вопросы о том, влиянием каких факторов — генетических или средовых — можно объяснить наблюдаемую изменчивость. Психологические признаки принадлежат к классу количественных признаков, законы наследования которых существенно отличаются от менделевских. Особая здесь и статистика.

Коэффициент наследуемости Хольцингера.

Для доказательства роли наследственности в развитии признака достаточно сравнить долю (процент) конкордантных пар у группах моно- и дизиготных близнецов. Для количественной оценки роли наследственности и внешней среды применяют различные формулы. Чаще всего пользуются коэффициентам наследственности (H) и влияния среды (E), вычисляемые по формуле Хольцингера:

Н2 = CМЗ-CДЗ/100-CДЗ

E =100 – H

CМЗ – процент конкордантности пар в группе монозиготных близнецов.

CДЗ – процент конкордантности пар в группах дизиготных близнецов.

Коэффициент наследуемости Игнатьева.

В качестве первой оценки величины генетической составляющей фенотипической дисперсии часто используется коэффициент Игнатьева. Данный способ оценки генетического компонента дисперсии и зарубежной психогенетике связан с именем Д. Фальконера, работа которого вышла в I960 г. Однако этот коэффициент был предложен еще в 1934 г. М.В. Игнатьевым.

Очевидно, что влияние любых факторов, изменяющих разницу между корреляциями двух типов близнецов (например, завышение корреляции между МЗ близнецами, возникающее в результате действия специфической для этого типа близнецов среды), будет влиять на оценку наследуемости. Хотя в последние годы появились и все чаще употребляются более современные и сложные методы статистического анализа, этот коэффициент, в силу своей аргументированности и простоты получения, остается в арсенале психогенетики.

Формула Игнатьева - формула для вычисления коэффициента наследуемости на основе коэффициентов корреляции близнецов:

Н2 = 2 (RМЗ - RДЗ), где R — коэффициент родства.

Теоретически ожидаемые корреляции между близнецами при генетической и средовой детерминации вариативности признака

  Действительно, если подставить значения коэффициентов корреляции, то максимальный показатель наследуемости, равный 1, мы получим в том случае, когда вариативность признака целиком определяется генами. В реальных ситуациях таких высоких коэффициентов практически не бывает, поскольку вариативность признака определяется не только генами, но и средой, причем различающаяся среда, как мы уже знаем, дает весьма существенный вклад в изменчивость психологических характеристик.

Анализ путей.

Приведенная выше логика разложения фенотипической дисперсии на ее составляющие, реализованная в нескольких эмпирических методах, представляет собой один из способов определения коэффициента наследуемости того или иного признака. Но понятие наследуемости можно также проанализировать при помощи «анализа путей».

Анализ путей в последние десятилетия широко используется и в психогенетике, и в науках о поведении вообще. Он был предложен генетиком С, Райтом еще в 30-х годах и затем им же и другими исследователями детально разработан.

Диаграмма путей — эвристичный способ наглядного графического представления причинных и корреляционных связей (путей) между переменными, позволяющий дать полное математическое описание линейной модели, которую применяют исследователи. Тем самым диаграмма путей способствует ее пониманию, верификации или представлению результатов. В целом путевые модели — «экстремально обобщенный» способ анализа, один из многих мультивариативных методов (к ним же относятся методы множественной регрессии, факторный и дискриминантный анализы и т.д.).

Существуют определенные правила построения диаграмм путей   (рис.   8.4).   Прямоугольники   (или   квадраты)   обозначают   наблюда емые переменные; круги (или эллипсы) — латентные, неизмеряемые переменные (на рис. 8.4. D и Е; А, В, С соответственно).

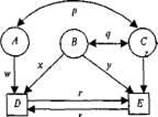
Рис. 8.4. Диаграмма путей, объединяющая три латентных (А, В, С) и две наблюдаемых (D и Е) переменных.

риq — корреляции; r, s, w, х, у, z — путевые коэффициенты.

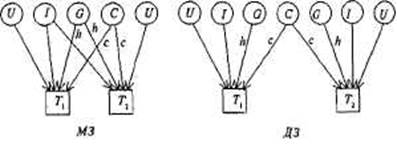Рис. 8.5. Диаграмма путей для корреляций совместно живущих пар МЗ и ДЗ близнецов.

Th т2 — близнецы одной пары. G — генотип; С— общая среда; U — индивидуальная (уникальная) среда; I— эпистаз. Пути h, с — влияния G, С на исследуемую черту.

Связи между переменными обозначаются стрелками: постулированные исследователем причинно-следственные — направленной в одну сторону («путь» от причины к следствию); наблюдаемые ассоциации — двусторонней. На рис. 8.4 первые — w, x, у, z, r, s (путевые коэффициенты); вторые — р и q (коэффициенты корреляции). Иначе говоря, модель выделяет зависимые переменные (D и Е), подлежащие объяснению или прогнозированию, и независимые (А, В, С), действие которых должно объяснить или предсказать зависимые переменные и их связи. Есть и другие, более детальные, правила оформления и чтения путевых диаграмм, но мы их рассматривать не будем.

На рис. 8.5 даны модели путей для корреляций совместно живущих пар МЗ и ДЗ близнецов по экстраверсии, из которых следует, что корреляция МЗ близнецов T1 и Т2 может быть выражена через сумму путей, связывающих их.

Несмотря на широкое использование этого метода и его достоинства, которые заключаются прежде всего в наглядной демонстрации представлений о компонентах, влияющих на исследуемый признак, он имеет и своих критиков. Так, Ф. Фогель и А. Мотульски «не уверены в том, что этот метод биометрического анализа внесет существенный вклад в наше понимание генетических факторов». Одно из главных сомнений вызывает тот факт, что в диаграмму путей и, следовательно, в дальнейший математический анализ закладываются уже имеющиеся у исследователя предположения о влияющих на признак факторах, их причинно-следственных отношениях и т.д., и результат анализа зависит, таким образом, от корректности заранее имеющихся исходных позиций.