Принцип, согласно которому законы физики должны быть одинаковы (инвариантны) с точки зрения любого наблюдателя, движущегося с постоянной скоростью, называется принципом относительности Галилея. Пусть у нас есть две системы отсчета: одна – неподвижная с координатами x, y, z и t, а другая, с координатами x¢, y¢, z¢ и t¢, движется относительно первой с постоянной скоростью V, направленной вдоль оси X. (Такие системы отсчета называются инерциальными).
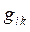
|
Центральным понятием принципа относительности является точечное событие, т.е. нечто происходящее в данной точке пространства (например, распад элементарной частицы, химическая реакция и т.д.). Любой физический процесс можно рассматривать как последовательность событий.
Координаты неподвижной и движущейся систем отсчета связаны преобразованиями Галилея (1):
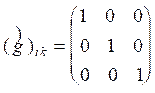 (1)
(1)
К электромагнитным явлениям принцип относительности Галилея неприменим. Рассмотрим пример. Пусть в системе (х, у, z) покоится электрический заряд. Согласно законам электростатики он создает вокруг себя электрическое поле. В то же время для наблюдателя, находящегося в системе (х¢, у¢, z¢), движущейся со скоростью v относительно первой системы, заряд движется и, следовательно, представляет собой электрический ток, который создает вокруг себя магнитное поле. В одной системе мы имели электрическое поле, а в другой получили электрическое плюс магнитное. Один и тот же объект в разных системах создает разные физические поля, что не согласуется с принципом Галилея.
Поскольку уравнения Максвелла не были инвариантными относительно преобразований Галилея, т.е. вопреки требованиям принципа относительности Галилея изменяли свою форму при переходе из одной инерциальной системы отсчета в другую, Лоренцем был поставлен естественный вопрос об отыскании таких преобразований координат и времени, которые не изменяли бы уравнений Максвелла и были при этом максимально простыми. Эта задача была им решена как чисто математическая (2):
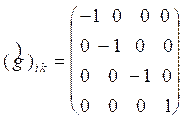 (2)
(2)
Сравнивая преобразования Галилея и Лоренца, легко заметить, что последние переходят в классические в случае скоростей, малых по сравнению со скоростью света с. Таким образом, предложенные Лоренцем соотношения удовлетворяли принципу соответствия, согласно которому новая теория должна согласовываться со старой в областях, где последняя была надежно проверена на экспериментах. Кроме того, следующий из преобразований Лоренца релятивистский закон сложения скоростей оставлял скорость света инвариантной относительно перехода в любую инерциальную систему отсчета, движущуюся со скоростью, меньшей С - скорости света в вакууме.
Поможем написать любую работу на аналогичную тему

