Основные выводы (следствия) СТО.

На основе сформулированных постулатов Эйнштейна пересматриваются все основные положения классической кинематики. Следствия специальной теории относительности называют релятивистскими эффектами:

1. Предсказываемый релятивистской теорией эффект замедления времени состоит в том, что с точки зрения движущегося относительно рассматриваемой системы наблюдателя все интервалы времени (t’), характеризующие процессы в этой системе (колебания маятников часов, распад нестабильных частиц, старение биологических организмов и т.д.) увеличиваются по сравнению с интервалами, наблюдаемыми в самой этой системе (). Для находящихся же в самой рассматриваемой системе наблюдателей происходящие в ней процессы протекают совершенно нормально, а время у движущегося наблюдателя "течет замедленно".

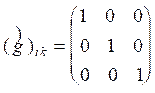                                                                                                                    (3)

2. Эффект сокращения расстояний состоит в уменьшении длин отрезков с точки зрения наблюдателей, перемещающихся вдоль(║)этих отрезков (отрезки, ориентированные перпендикулярно (^) скорости относительного движения сохраняют свою длину неизменной):

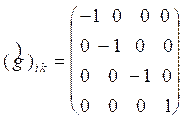                                                                                                                        (4)

3. Относительность одновременностей.

Пусть в системе отсчета К' происходят два одновременных события с координатами х1', t' и х2', t'. Вычислим разность их временных координат в системе К (с точки зрения неподвижного наблюдателя). Из преобразований Лоренца (2), выражающих t через t' и х1', легко получить:

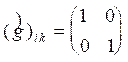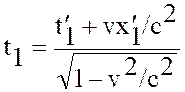,   .                                        (5)

Если принять во внимание, что t2'=t' и t1'=t' (события одновременные), т.е. t2'=t1=0, то получаем:

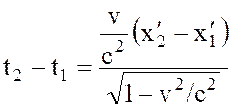.                                                                    (6)

Т.е. одновременные события в движущейся системе К' для неподвижного наблюдателя в системе К неодновременны.

4.Закон сложения скоростей

В классической механике скорость тела просто складывается со скоростью системы отсчета. В теории относительности скорость преобразуется по более сложному закону.

Пусть две системы К и К¢ наблюдают за движением некоторого тела, которое перемещается равномерно и прямолинейно параллельно осям х и х' обеих систем отсчета. Пусть скорость тела, измеренная системой отсчета К, есть u: скорость того же тела, измеренную системой К¢ обозначим через и'. Буквой v будем обозначать  скорость системы  К¢ относительно К.

Допустим, что с телом происходят два события, координаты которых в системе К суть х1, t1 и х2, t2. Координаты тех же событий в системе К¢ пусть будут х1¢, t1¢ и х2¢, t2¢. Но скорость тела есть отношение пройденного телом пути к соответствующему промежутку времени, поэтому, чтобы найти скорости тела в той и другой системах отсчета, нужно разность пространственных координат обоих событий разделить на разность временных координат:

;   .

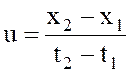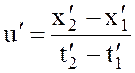Из преобразований Лоренца легко получить следующее:

;

.

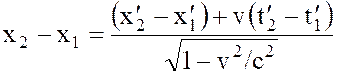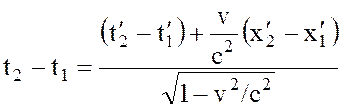Поделив первое на второе, получим:

;

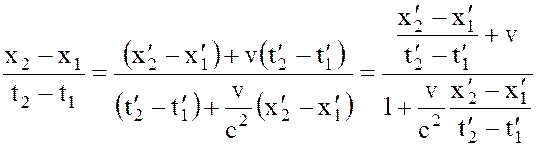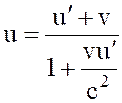.                                                                                       (7)

Это и есть релятивистский закон сложения скоростей. Он заменяет собой классическую формулу

,

которую можно как всегда получить из релятивистской, если скорость света считать c >> v.

Если рассматривать случай, когда система отсчета К движется относительно К¢ со скоростью -v, тогда можно записать, заменив u на u¢:

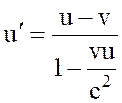                                                                                         (8)

Если скорость тела, например, u¢ равна скорости света с, то имеем:

.

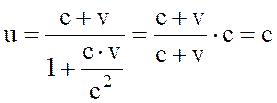Это есть не что иное, как закон постоянства скорости света, согласно которому закон сложения скоростей эквивалентен постулату постоянной скорости и света.

Преобразования Лоренца занимают в теории относительности весьма важное место, составляя одну из математических ее основ.

Описанные эффекты проявляются лишь при скоростях, сравнимых со скоростью света и в настоящее время экспериментально зарегистрированы в пучках ультарелятивискских частиц, создаваемых на современных ускорителях. Например, короткоживущие частицы (время жизни ), двигаясь с околосветовыми скоростями, вопреки классическим представлениям достигают приемника, удаленного на расстояние, значительно превышающее . С точки зрения неподвижного наблюдателя это явление можно объяснить эффектом замедления времени, "удлиняющим" жизнь частицы, с точки зрения наблюдателя, движущегося вместе с частицей - эффектом сокращения расстояния до мишени, "летящей ему навстречу".

С эффектом замедления времени часто ошибочно связывают "парадокс близнецов" - утверждение о том, что двигавшийся с околосветовыми скоростями космический путешественник должен вернуться на Землю менее постаревшим, чем его брат, оставшийся дома. Кажущийся парадокс связан с тем, что в силу относительности равномерного движения с точки зрения космического путешественника эффект замедления времени должен наблюдаться на самой Земле. Реального противоречия не возникает, поскольку для того, чтобы возвратиться домой, космонавт должен в течение определенного времени двигаться с ускорением (тормозить, разворачивать корабль, вновь ускоряться), что нарушает симметрию между ним и наблюдателем на Земле (ускорение носит абсолютный характер). Адекватное описание явлений, происходящих в ускоренно движущихся системах отсчета, выходит за рамки СТО и составляет предмет Общей Теории Относительности.