Таблица частот и функции распределения.

Цель. Таблицы частот или одновходовые таблицы представляют собой простейший метод анализа категориальных (номинальных) переменных (см. Элементарные понятия статистики). Часто их используют как одну из процедур разведочного анализа, чтобы просмотреть, каким образом различные группы данных распределены в выборке. Например, изучая зрительский интерес к разным видам спорта (с целью рекламы какого-либо продукта на ТВ), вы могли бы представить ответы респондентов следующей таблицей:

Таблица показывает частоты, кумулятивные (накопленные) частоты, процент, кумулятивный процент респондентов, выразивших свой интерес к просмотру футбольных матчей в следующей шкале: (1) Всегда интересуюсь, (2) Обычно интересуюсь, (3) Иногда интересуюсь или (4) Никогда не интересуюсь.

Приложения. Практически каждый исследовательский проект начинается с построения таблиц частот. Например, в социологических опросах таблицы частот могут отображать число мужчин и женщин, выразивших симпатию тому или иному политическому деятелю, число респондентов из определенной этнических групп, голосовавших за того или иного кандидата и т.д. Ответы, измеренные в определенной шкале (например, в шкале: интерес к футболу) также можно прекрасно свести в таблицу частот. В медицинских исследованиях табулируют пациентов с определенными симптомами. В маркетинговых исследованиях - покупательский спрос на товары разного типа у разных категорий населения. В промышленности - частоту выхода из строя элементов устройства, приведших к авариям или отказам всего устройства при испытаниях на прочность (например, для определения того, какие детали телевизора действительно надежны после эксплуатации в аварийном режиме при большой температуре, а какие нет). Обычно, если в данных имеются группирующие переменные, то для них всегда вычисляются таблицы частот.

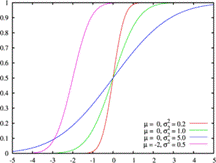
Определение. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ— плотность вероятности распределения частиц макроскопической системы по координатам, импульсам или квантовым состояниям. Функция распределения является основной характеристикой самых разнообразных (не только физических) систем, которым свойственно случайное поведение, т. е. случайное изменение состояния системы и, соответственно, ее параметров. Даже в стационарных внешних условиях само состояние системы может быть таким, что результат измерения некоторого его параметра является случайной величиной. Функция распределения в подавляющем большинстве случаев содержит в себе всю возможную и потому исчерпывающую информацию о свойствах таких систем.

Функцией распределения называют функцию F(x), определяющую вероятность того, что случайная величина Х в результате испытания примет значение, меньшее х.

            Функцию распределения также называют интегральной функцией.

Функция распределения существует как для непрерывных, так и для дискретных случайных величин. Она полностью характеризует случайную величину и является одной из форм закона распределения.

            Для дискретной случайной величины функция распределения имеет вид:

            Знак неравенства под знаком суммы показывает, что суммирование распространяется на те возможные значения случайной величины, которые меньше аргумента х.

            Функция распределения дискретной случайной величины Х разрывна и возрастает скачками при переходе через каждое значение хi.

   Так для примера, рассмотренного выше, функция распределения будет иметь вид:

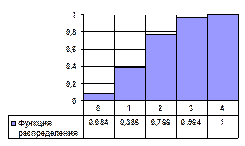Свойства функции распределения

            1) значения функции распределения принадлежат отрезку  .

            2) F(x) – неубывающая функция.

 при

            3) Вероятность того, что случайная величина примет значение, заключенное в интервале (a, b) , равна приращению функции распределения на этом интервале.

            4) На минус бесконечности функция распределения равна нулю, на плюс бесконечности функция распределения равна единице.

            5) Вероятность того, что непрерывная случайная величина Х примет одно определенное значение, равна нулю.

            Таким образом, не имеет смысла говорить о каком – либо конкретном значении случайной величины. Интерес представляет только вероятность попадания случайной величины в какой – либо интервал, что соответствует большинству практических задач.

Нормальное распределение (этот термин был впервые использован Гальтоном в 1889 г.), также иногда называемое гауссовским, определяется следующим образом:

f(x) = 1/ * e**{-1/2*2}

-Ґ < x < Ґ

где

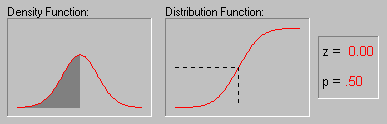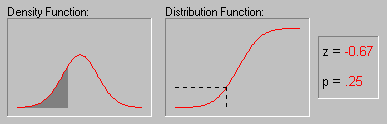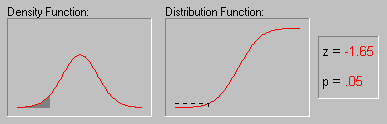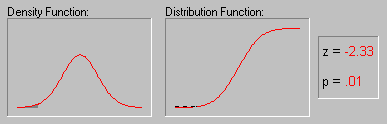
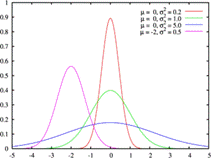
Нормальное распределение, также называемое распределением Гаусса, — распределение вероятностей, которое играет важнейшую роль во многих областях знаний, особенно в физике. Физическая величина подчиняется нормальному распределению, когда она подвержена влиянию огромного числа случайных помех. Ясно, что такая ситуация крайне распространена, поэтому можно сказать, что из всех распределений в природе чаще всего встречается именно нормальное распределение — отсюда и произошло одно из его названий.

Нормальное распределение зависит от двух параметров — смещения и масштаба, то есть является с математической точки зрения не одним распределением, а целым их семейством. Значения параметров соответствуют значениям среднего (математического ожидания) и разброса (стандартного отклонения).

Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием 0 и стандартным отклонением 1.

Вероятность того, что рост произвольного человека попадет в определенный выбранный нами диапазон, будет зависеть от трех факторов.

Во-первых, от величины такого диапазона - чем точнее наши требования, тем меньше вероятности, что нам повезет.

Во-вторых, от того, насколько "популярен" выбранный нами рост. Напомним, что мода - самое часто встречающееся значение роста. Кстати для нормального распределения мода, медиана и среднее значение совпадают. Кривая нормального распределения симметрична относительно среднего значения. И, в-третьих, вероятность попадания роста в определенный диапазон зависит от характеристики рассеивания случайной величины. Отчасти это связано с единицами измерения (представьте, что мы бы измеряли людей в дюймах, а не в миллиметрах, но сами люди и их рост были бы теми же). Но дело не только в этом. Просто некоторые процессы кучнее группируются возле среднего значения, в то время как другие более разбросаны. Например, рост собак и рост домашних кошек имеют разный разброс значений, их кривые нормального распределения будут выглядеть по-разному (напомним еще раз, что площадь под обеими кривыми будет единичной). Так, кривая для роста кошек будет более узкой и высокой, а для роста собак кривая будет ниже и шире.

Для характеристики разброса конечного ряда данных в прошлом разделе мы использовали величину среднего квадратического отклонения. Аналогичная величина используется для характеристики кривой нормального распределения. Она обозначается буквой s и называется в этом случае стандартным отклонением.