Нечеткие множества

Пусть E - универсальное множество, x - элемент E, а R - определенное свойство. Обычное (четкое) подмножество A универсального множества E, элементы которого удовлетворяют свойство R, определяется как множество упорядоченной пары A = {mA (х)/х}, где mA(х) - характеристическая функция, принимающая значение 1, когда x удовлетворяет свойство R, и 0 - в другом случае.

Нечеткое подмножество отличается от обычного тем, что для элементов x из E нет однозначного ответа "нет" относительно свойства R. В связи с этим, нечеткое подмножество A универсального множества E определяется как множество упорядоченной пари A = {mA(х)/х}, где mA(х) - характеристическая функция принадлежности (или просто функция принадлежности), принимающая значение в некотором упорядоченном множестве M (например, M = ).

Функция принадлежности указывает степень (или уровень) принадлежности элемента x к подмножеству A. Множество M называют множеством принадлежностей. Если M = {0,1}, тогда нечеткое подмножество A может рассматриваться как обычное или четкое множество.

Рассмотрим множество X всех чисел от 0 до 10. Определим подмножество A множества X всех действительных чисел от 5 до 8.

A =

Покажем функцию принадлежности множества A, эта функция ставит в соответствие число 1 или 0 каждому элементу в X, в зависимости от того, принадлежит данный элемент подмножеству A или нет. Результат представлен на следующем рисунке:

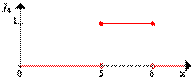
Можно интерпретировать элементы, соответствующие 1, как элементы, находящиеся в множестве A, а элементы, соответствующие 0, как элементы, не находящиеся в множестве A.

Эта концепция используется в многих областях. Но существуют ситуации, в которых данной концепции будет не хватать гибкости.

В данном примере опишем множество молодых людей. Формально можно записать так

B = {множество молодых людей}

Поскольку, вообще, возраст начинается с 0, то нижняя граница этого множества должна быть нулем. Верхнюю границу определить сложнее. Сначала установим верхнюю границу, скажем, равную 20 годам. Таким образом, имеем B как четко ограниченный интервал, буквально: B = . Возникает вопрос: почему кто-то в свой двадцатилетний юбилей - молодой, а сразу на следующий день уже не молодой? Очевидно, это структурная проблема, и если передвинуть верхнюю границу в другую точку, то можно задать такой же вопрос.

Более естественный путь создания множества B состоит в ослаблении строгого деления на молодых и не молодых. Сделаем это, вынося не только четкие суждения "Да, он принадлежит множеству молодых людей" или "Нет, она не принадлежит множеству молодых людей", но и гибкие формулировки "Да, он принадлежит к довольно молодым людям" или "Нет, он не очень молодой".

Рассмотрим как с помощью нечеткого множества определить выражение "он еще молодой".

В первом примере мы кодировали все элементы множества с помощью 0 ли 1. Простым способом обобщить данную концепцию является введение значений между 0 и 1. Реально можно даже допустить бесконечное число значений между 0 и 1, в единичном интервале I = .

Интерпретация чисел при соотношении всех элементов множества становится теперь сложнее. Конечно, число 1 соответствует элементу, принадлежащему множеству B, а 0 означает, что элемент точно не принадлежит множеству B. Все другие значения определяют степень принадлежности к множеству B.

Для наглядности приведем характеристическую функцию множества молодых людей, как и в первом примере.

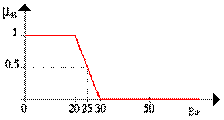
Пусть E = {x1, x2, x3, x4, x5 }, M = ; A - нечеткое множество, для которого

mA(x1)=0,3; mA(x2)=0; mA(x3)=1; mA(x4)=0,5; mA(x5)=0,9

Тогда A можно представить в виде:

A = {0,3/x1; 0/x2; 1/x3; 0,5/x4; 0,9/x5 } или

A = 0,3/x1 + 0/x2 + 1/x3 + 0,5/x4 + 0,9/x5,

(знак "+" является операцией не сложения, а объединения) или