Операции над нечеткими множествами

Содержание

Пусть A и B - нечеткие множества на универсальном множестве E.

Говорят, что A содержится в B, если "x ÎE mA(x) <mB(x).

Обозначение: A Ì B.

Иногда используют термин "доминирование", то есть в случае если A Ì B, говорят, что B доминирует A.

Равенство

A и B равны, если "xÎE mA(x) = mB (x).

Обозначение: A = B.

Дополнение

Пусть M = , A и B - нечеткие множества, заданные на E. A и B дополняют друг друга, если

"xÎE mA(x) = 1 - m B(x).

Обозначение: B = или A =

Очевидно, что = A. (Дополнение определено для M = , но очевидно, что его можно определить для любого упорядоченного M).

Пересечение

AÇB - наибольшее нечеткое подмножество, которое содержится одновременно в A и B.

mAÇB(x) = min( mA(x), mB(x)).

Объединение

А È В - наименьшее нечеткое подмножество, которое включает как А, так и В, с функцией принадлежности:

mAÈ B(x) = max(mA(x), m B(x)).

Разность

А - B = АÇ с функцией принадлежности:

mA-B(x) = mA Ç (x) = min( mA(x), 1 - m B(x)).

Дизъюнктивная сумма

АÅB = (А - B)È(B - А) = (А Ç ) È( Ç B) с функцией принадлежности:

mA-B(x) = max{; }

Наглядное представление операций над нечеткими множествами

Для нечетких множеств можно применить визуальное представление. Рассмотрим прямоугольную систему координат, на оси ординат которой откладываются значение mA(x), на оси абсцисс в произвольном порядке расположены элементы E. Если E по своей природе упорядочено, то этот порядок желательно сохранить в расположении элементов на оси абсцисс. Такое представление делает наглядными простые операции над нечеткими множествами.

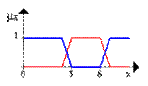
Пусть A нечеткий интервал между 5 до 8 и B нечеткое число около 4, как показано на рисунке.

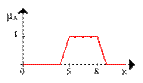
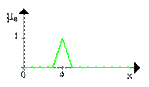
Проиллюстрируем нечеткое множество между 5 и 8 И (AND) около 4 (синяя линия).

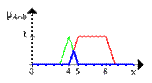
Нечеткое множество между 5 и 8 ИЛИ (OR) около 4 показано на следующем рисунке (снова синяя линия).

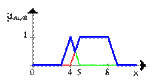
Следующий рисунок иллюстрирует операцию отрицания. Синяя линия - это ОТРИЦАНИЕ нечеткого множества A.