Одним из мощных инструментов решения большого класса задач является анализ безубыточности производства. Посредством такого анализа можно определять точку безубыточности, планировать целевой объем производства, устанавливать цены на продукцию, осуществлять выбор наиболее эффективных технологий производства, разрабатывать оптимальные производственные планы.
Как известно, существует две модели анализа безубыточности: экономическая и бухгалтерская . При помощи теоретической зависимости выручки от реализации, затрат и прибыли от объема производства строится экономическая модель, позволяющая создать основы бухгалтерской модели и выяснить механизм ее действия
Экономическая модель поведения затрат, объема производства и прибыли представлена на рис. 1. В соответствии с данной моделью предприятие может наращивать объемы продаж только путем уменьшения цены реализации единицы продукции, в результате чего линия выручки от реализации, возрастающая вначале, постепенно замедляет подъем, а затем опускается вниз. Это связано с тем, что в определенный момент положительный эффект от увеличения объема продаж оказывается ниже отрицательного влияния снижения цен.
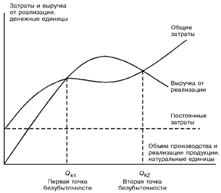
Как видно из рис. 1, линия выручки от реализации пересекает линию общих затрат в двух точках. Это означает, что в экономической модели без-убыточности существует два уровня выпуска и реализации продукции, при которых общие затраты равны выручке от реализации, т.е. две точки безубыточности. На поведение совокупных затрат в этой модели наиболее сильное влияние оказывают переменные издержки, изменяющиеся в соответствии с известным эффектом масштаба.
При построении бухгалтерской модели делается допущение о неизменности переменных издержек и цены реализации единицы продукции, в результате чего зависимость выручки от реализации и общих затрат от изменения объема производства и реализации имеет линейный характер. Диаграмма безубыточности по бухгалтерской модели отражена на рис. 2.
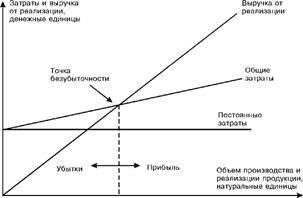
Из рис. 2 видно, что в бухгалтерской модели, в отличие от экономической, - одна, а не две точки безубыточности. Поэтому с увеличением объема производства зона прибыли расширяется и наиболее прибыльным становится производство при максимальной загрузке производственных мощностей.
При анализе безубыточности по бухгалтерской модели используется не только графический, но и математический подход к отражению и обработке исходной информации о затратах и результатах деятельности предприятия . В соответствии с данной моделью математическая зависимость между прибылью, объемом производства и затратами имеет следующий вид:
PR = pq - c - vq, (1)
где PR - прибыль от реализации продукции, денежных единиц;
p - цена реализации единицы продукции, денежных единиц;
q - количество проданных единиц продукции, натуральных единиц;
c - совокупные постоянные затраты, денежных единиц;
v - переменные затраты на единицу продукции, денежных единиц.
На основе формулы (1) легко проводится решение основных задач анализа безубыточности: определение точки безубыточности; определение объемов производства для получения целевой прибыли; определение цены в анализе безубыточности.
Точка безубыточности - это такой объем продукции, при реализации которого выручка от реализации покрывает совокупные затраты. В этой точке выручка не позволяет предприятию получить прибыль, однако убытки тоже отсутствуют. В соответствии с чем согласно (1) формула для определения точки безубыточности Qk примет следующий вид:
![]() (2)
(2)
Анализ безубыточности позволяет определить количество единиц продукции Qпл, которое необходимо произвести и реализовать для получения запланированной прибыли PRпл. Исходя из (1) искомый объем продукции Qпл определяется следующим образом:
![]() (3)
(3)
С помощью анализа безубыточности можно также принимать и ценовые решения. На основе (1) (учитывая, что в точке безубыточности PR = 0) минимально допустимая цена за единицу продукции, обеспечивающая покрытие совокупных затрат, будет определяться следующим образом:
![]() (4)
(4)
Формула (4) служит отправной для расчета цены, которую требуется установить для получения запланированного размера прибыли PRпл:
![]() (5)
(5)
Следует отметить, что математический аппарат для проведения анализа безубыточности разработан лишь применительно к бухгалтерской модели, на основе которой и ведутся все практические расчеты . Вместе с тем допущения, положенные в основу данной модели, могут искажать достоверность результатов проводимого анализа.
К числу наиболее существенных в бухгалтерской модели относится предположение о неизменности цены реализации единицы продукции. С точки зрения адекватности действительности такое допущение не всегда приемлемо для предприятий. Это подтверждают, в частности, результаты авторского мониторинга ряда организаций г. Благовещенска, когда изменение цен на продукцию последних вызывало моментальную ответную реакцию рынка. В подобных условиях, характеризующихся высокой степенью ценовой эластичности спроса, применение бухгалтерской модели безубыточности ведет к некорректному решению соответствующих маркетинговых задач, в связи с чем представляется актуальным поиск более совершенных подходов к решению рассматриваемой проблемы.
С целью проведения анализа безубыточности, свободного от ряда допущений, положенных в основу бухгалтерской модели, автором разработан и представлен ниже соответствующий математический инструментарий.
Базовым выражением для проведения анализа безубыточности является формула для определения прибыли от реализации продукции, представленная следующим образом:
PR(q, х1, х2, ... , хn, y1, y2, ... , ym) = P(х1, х2, ... , хn)q -С(y1, y2, ... , ym), (6)
где P(х1, х2,...,хn) - функция зависимости цены единицы продукции от влияющих на нее факторов (где х1, х2,..., хn - факторы, учитываемые в модели, n - число таких факторов);
С(y1, y2,..., ym) - функция общих затрат (где y1, y2,..., ym - факторы, учитываемые в модели, m - число таких факторов).
Далее показано применение выражения (6) для решения основных задач анализа безубыточности.
Так как безубыточным является объем, при котором выручка от реализации равна совокупным затратам, формула для определения точки безубыточности Qk согласно (6) примет следующий вид:
![]() (7)
(7)
При этом при проведении расчетов для определения прогнозного значения рыночной цены продукции в эмпирическую функцию P(х1, х2,..., хn) подставляются прогнозные значения соответствующих факторов.
В соответствии с выражением (7) объем продукции Qпл, который предприятию необходимо произвести и реализовать для получения запланированного размера прибыли PRпл, определится по следующей формуле:
![]() (8)
(8)
Для расчета цены, установление которой обеспечивает получение запланированного размера прибыли PRпл, необходимо найденный из формулы (8) объем продукции Qпл подставить в функцию P(х1, х2,..., хn).
Согласно предпосылкам описываемого подхода рост объема производства и реализации сопровождается постоянным снижением цены. Поэтому минимально допустимая цена за единицу продукции, обеспечивающая покрытие совокупных затрат, будет соответствовать второй точке безубыточности; максимально допустимая - первой точке безубыточности. Аналитически определение данных цен осуществляется путем соответствующих подстановок рассчитанного по формуле (7) безубыточного объема производства в функцию P(х1, х2,..., хn).
Однако заметим, что формула для определения прибыли от реализации продукции может быть представлена также с использованием функции зависимости объема спроса от влияющих на него факторов Q(х1, х2,..., хn) (вместо функции зависимости цены единицы продукции от совокупности факторов, определяющих ее величину):
PR(q, х1, х2, ... , хn, y1, y2, ... , ym) = Q(х1, х2, ... , хn)p - С(y1, y2, ... , ym). (9)
Выбор того или иного признака (цены либо объема спроса) в качестве результативного (что в итоге определяет дальнейшее проведение анализа по формуле (6) либо по формуле (9)) актуален, прежде всего, для случая множественной регрессии. Это связано, в основном, с трудностями математического плана, возникающими при построении многофакторных моделей. В частности, при построении таких моделей нередко приходится сталкиваться с проблемой мультиколлинеарности, т.е. такой ситуацией, при которой между факторными признаками может существовать значительная линейная связь, что приводит в конечном счете к недопустимому росту ошибок оценок регрессии . Одним из способов решения данной проблемы является выбор соответствующего фактора в качестве результативного, а также должный отбор включаемых в модель регрессоров.
В случае, если формула для определения прибыли от реализации продукции определена в виде (9), анализ безубыточности проводится следующим образом. Критическая (т.е. минимально и максимально допустимая) цена находится по формуле
![]() (10)
(10)
Цена единицы продукции, которую требуется установить для получения запланированного размера прибыли PRпл, находится с применением следующей формулы:
![]() (11)
(11)
В силу того, что функция общих затрат в любом случае зависит от объема производства и реализации q, для сведения формул (10) и (11) к уравнениям с одной неизвестной, необходимо произвести замену величины q на функцию зависимости данной величины от влияющих на нее факторов, т.е. на Q(х1, х2, ... , хn).
Точка безубыточности находится путем подстановки найденной из формулы (10) критической цены Pк в функцию Q(х1, х2,..., хn). При подстановке в данную функцию величины Pпл определяется количество единиц продукции Qпл, которое необходимо произвести и реализовать для получения прибыли на запланированном уровне.
Следует отметить, что именно представление формулы для определения прибыли от реализации продукции в виде (6) либо (9), а не в жестко детерминированном с постоянными значениями переменных затрат и цен на единицу продукции, позволяет преодолеть основные допущения бухгалтерской модели безубыточности.
Выражения (6) и (9) описывают общий случай зависимости прибыли от реализации продукции от влияющих на нее факторов. На их основе, с учетом конкретных условий и особенностей функционирования предприятий, а также с учетом степени дефицита маркетинговой и иной информации, легко выводятся частные и единичные случаи анализируемой зависимости. Так, в случае, когда функция зависимости цены единицы продукции определена в виде P(q) (т.е. предполагается, что на цену влияет только объем продаж) и функция общих затрат представлена в виде С(q), формула (6) является математической интерпретацией экономической модели безубыточности. Аналогичным образом описывает данную модель и формула (9), когда функция спроса представлена в виде Q(p), а функция общих затрат - в виде С(q).
Вместе с тем, и это необходимо отметить, не отрицается возможность и правомерность использования (в соответствующих условиях) бухгалтерской модели безубыточности, которая также рассматривается как частный случай выражений (6) и (9), когда переменные издержки на единицу продукции и цена реализации постоянны.
Цена(Ц)*V-м выпуска(Q)=Пост. издержки(Ипост)+Перем. изд-ки на ед-цу прод-ии(И1перем)*Q;
Ц*Q-И1перем*Q=Ипост;
Q(Ц-И1перем)=Ипост;
Q(V-м пр-ва в т. беззуб-ти)=![]()
Q(v-м пр-ва при задан. ур-не прибыли)=![]() , (Пн – необх. прибыль)
, (Пн – необх. прибыль)
Точку беззуб-ти можно определить и графически.

Поможем написать любую работу на аналогичную тему

