Разомкнутые процессы.

Сжатие и расширение любого рабочего тела при обратимом проведении процесса может характеризоваться энергетическим и эксергетическим балансами. Рассмотрим в качестве примера процесс сжатия.

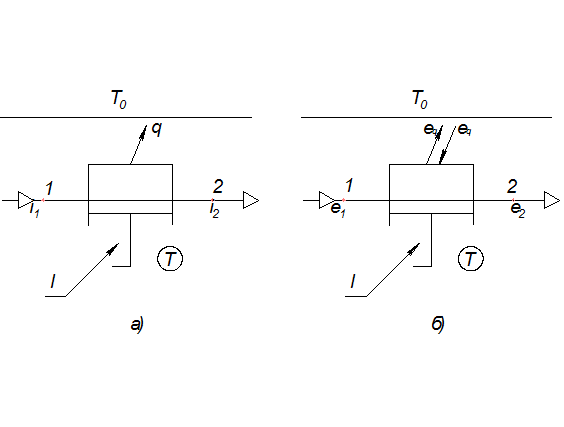Рис. 4.2. Схема процесса сжатия.

а – энергетический баланс

б – эксергетический баланс.

Пользуясь первым законом термодинамики и принимая во внимание, что D=0 и ΔE=0 (процесс обратимый и стационарный), получаем следующие  уравнения:

Уравнение энергетического баланса:

Уравнение эксергетического баланса:

В зависимости от знака τe, определяемого соотношением температур T и T0 ,величина eq может быть как положительной, так и отрицательной.

Рассмотрим приведенные соотношения при T=T0. В этом случае   τe = 0 и eq = 0, следовательно, l = e2 - e1, т. е. работа изотермического сжатия при температуре окружающей среды равна разности эксергий в начальном и конечном состояниях.

В диаграмме i-e изотермический процесс сжатия представляется следующим образом:

                                                   Т0

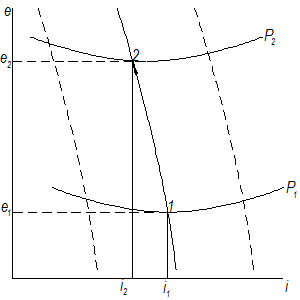
   Рис.4.3. Процесс изотермического сжатия при Т = Т0

Из уравнения энергетического баланса следует, что изменение энергии газа равно разности  между затраченной работой и отведённым теплом

.

Для идеального газа эта величина равна нулю,     поскольку его энергия не зависит от давления и отведённое в процессе сжатия тепло q  равно затраченной работе l.

Для реального газа в общем случае l ≠ q и значение разности i2 - i1 определяется величиной изотермического дроссель-эффекта  ΔiT, который при данной температуре равен  ΔiT = i1 - i2 .

 С учетом дроссель-эффекта уравнение энергетического баланса процесса сжатия:

l = q- ΔiТ

Выразим q из данного уравнения (q = l + ΔiT ) и подставим в уравнение эксергетического баланса  l = e 2  -   e1   +   eq   =   Δe   +   q τe    значения q и τe.

В результате подстановки получим:

Преобразуем:

Разделим уравнение почленно на , получим:

    или                 

и                                   

Формулы для определения l и q действительны как при T>T0 так и при T<T0. Определив с помощью диаграммы i-e  величину e и ΔiT, можно найти значения l и q.

 Для идеального газа ΔiT = 0 и выражение для l и q сводится к формуле

Диаграмма i-e  дает возможность производить расчеты, связанные с теплообменом. Для этого  используют зависимость, связывающую эксергетическую температурную функцию и эксергию потока. Она получится следующим образом.

 Рассмотрим е как функцию i, p.  

Тогда

; 

  С другой стороны          .

Расшифруем значение ds:

 и подставим в выражение для de

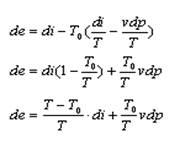
Сравним с de, получим               

 т.е. частная производная термомеханической эксергии  потока по энтальпии при постоянном давлении равна эксергетической температурной функции.

Поскольку (∂i)p = δq, то с учётом  уравнения eq = Σδq τе    после  подстановки получаем

                                         (∂е)Р = δq τе = δeq.

Для конечного изобарного процесса

                                         (Δе)Р = еq

                Изменение эксергии потока рабочего тела  е в изобарном процессе равно эксергии еq связанного с  этим процессом теплового потока q.

Используя эту зависимость, можно найти эксергию тепла еq для любого изменения состояния при p=const.