При сравнении вариантов по формуле 
предполагается, что капитальные вложения осуществляются единовременно (мгновенно), после чего начинается эксплуатация объекта с равными по времени издержками до бесконечности (в состав издержек включены амортизационные исчисления).
В действительности капитальные вложения как правило осуществляются в течение некоторого времени, варианты могут отличаться по продолжительности реализации или строительства, а также различаться по распределению затрат (как единовременных, так и текущих) во времени. Затраты, осуществляемые в различные моменты времени не равноценны между собой, т.к. капитал, пущенный в оборот, приносит доход.
Основным методическим приемом для применения разновременных затрат капитала в сопоставимый вид является приведение их к одному моменту времени, в качестве которого может выбираться момент начала, окончания строительства, промежуточный или любой другой момент времени.
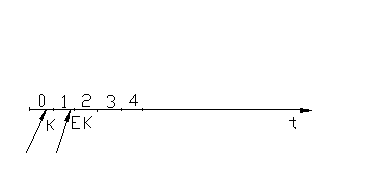Если капитальные вложения осуществляются в течение одного года, то мы не несем никаких издержек от изъятия капитала из оборота.
Начальный момент времени – нулевой год – служит для облегчения математических преобразований.
Если в течение первого года капитальные вложения заморожены (не дают эффекта), то владелец капитала несет дополнительный ущерб от недоиспользования капитала в размере ЕК. Поэтому к концу первого – началу второго года капитальные вложения будут равняться:
При неиспользовании капитальных вложений в течение двух лет, т.е. к концу второго – началу третьего года приведенные капитальные вложения составят:
По аналогии при сроке строительства, равном Т, приведенные капитальные вложения будут равняться:
Если строительство осуществлялось в течение трех лет в размере капиталовложения Ко, К1, К2, то приведенные капиталовложения будут равняться:
В общем случае при приведении капитальных вложений к моменту времени Т они будут иметь вид:
В результате приведения капитальных вложений к конечному моменту времени приводит к увеличению их величины, которая становится больше суммарной (сметной) стоимости объекта. При этом стоимость объекта не меняется, а величина приведенных затрат является всего лишь абстракцией, используемой только для сравнения вариантов. Если суммарная стоимость объекта равна 
, и строительство велось в течение некоторого времени, то в начальный момент времени владелец капитала может располагать суммой меньше, чем 
, и совместно с использованием дохода от оборота временно свободного капитала он может реализовать данный вариант.
Допустим, строительство переносится на один год и ведется в течение первого года, то к начальному моменту времени можно располагать суммой:
,
которой бы совместно с доходом от оборота капитала в нулевой год хватило бы для реализации проекта. Рассуждая аналогично, получим капитальные вложения, приведенные к начальному моменту времени, равные:
.
Т.е. общая формула:
Таким образом, приведенные к начальному моменту времени капитальные вложения – это та сумма, которой необходимо располагать, которая совместно с эффектом от оборота временно свободного капитала хватило бы для реализации проекта.
При сравнении вариантов приведение всегда осуществляется к одному и тому же моменту времени.
Допустим, 
.
Разделим обе части на 
, и в результате получим:
, и соотношение не изменится.
Если одновременно со строительством объекта начинается частичная эксплуатация его с издержками И, то приведенные затраты 
будут записаны:
.
С точки зрения владельца капитала различные категории затрат (единовременные или текущие) равноценны между собой, если они осуществляются в один и тот же момент времени.
Принципы формирования динамических критериев оптимальности
1. Первый тип объектов: строительство осуществляется в течение одного года (единовременно), после чего начинается эксплуатация объекта с равными по годам издержками. В состав издержек включаются амортизационные отчисления, поэтому теоретически эксплуатация продолжается бесконечно.
Величина 
, поэтому можно записать:
.
Под знаком суммы у нас находится бесконечно убывающая геометрическая прогрессия, сумма членов которой равняется 
.
а – первый член прогрессии;
q – знаменатель геометрической прогрессии.
В нашем случае 
.
В результате:
.
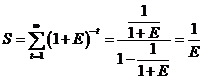В итоге приведенные затраты для первого типа объектов будут равняться:
.
Деление издержек на коэффициент дисконтирования (норму доходности капитала) называют капитализацией издержек, так же, как и капитализацию прибыли.
Т.к. абсолютная величина приведенных затрат нас не интересует – это абстракция, используемая только для сравнения вариантов, - то полученное выше значение мы можем умножить на коэффициент дисконтирования и получить формулу приведенных затрат в виде:
2. Второй тип объектов: капиталовложения осуществляются в течении нескольких лет Т, после чего начинается эксплуатация с равными по годам и бесконечными во времени издержками (издержки нормального периода эксплуатации).
.
Под знаком суммы находится бесконечно убывающая геометрическая прогрессия, первый член которой равен 
, а знаменатель – 
.
Тогда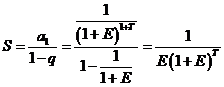 
.
В результате:
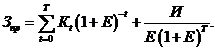
Приводим данную величину приведенных затрат к моменту окончания строительства. Для этого умножаем полученное выражение на 
, и получаем приведенные затраты в виде:
По аналогии с первым случаем умножаем полученное выражение на коэффициент дисконтирования и получаем для сравнения критерий в виде:
.
3. Третий тип объектов: одновременно со строительством начинается частичная эксплуатация объекта (формула профессора Болотова):
.
Выполняя аналогичные преобразования, получаем:
.
В этой формуле есть подвох, связанный со временем окончания строительства. При сравнении вариантов с разными моментами окончания строительства приведение по формуле Болотова осуществляется к моменту более позднего окончания строительства, либо еще более позднему сроку, но никак не к раннему.
Если издержки представить в виде 
, где дельта 
– это приращение издержек производства от момента времени t к моменту времени t + 1, т.е 
, то после преобразований получим:
- эта формула – для истории.
4. Четвертый тип объектов: бесконечно развивающиеся объекты.
(1)
Данный критерий невозможен для применения из-за отсутствия четкого определения периода расчета. Поэтому выбор расчетного периода оптимизации непрерывно развивающихся объектов можно производить, исходя из условия равенства ошибки расчетов из-за ненадежности информации, относительно перспективных экономических показателей, и ошибки расчетов из-за неучета затрат за пределами расчетного периода. Равные затраты последующих лет из-за влияния фактора времени уменьшаются в геометрической прогрессии.
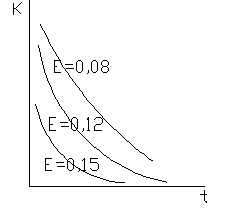
Задаваясь определенной точностью определения приведенных затрат, можно не учитывать все затраты, за пределами расчетного периода, если они увеличивают конечное выражение приведенных затрат в пределах заданной точности расчетов. Теперь в формуле (1) можно поставить вместо бесконечности – T.
Поможем написать любую работу на аналогичную тему